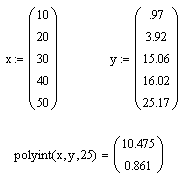
|
Pers.narod.ru. Обучение. Полиномиальная интерполяция в MathCAD |
Возможности, описанные в статье, полностью доступны в MathCAD версии 14 и выше. Ссылка на теорию и реализация задачи средствами программирования в MathCAD находятся здесь.
А в современных версиях всё можно сделать с помощью трёх встроенных функций.
Функция polyint(X,Y,x) выполняет полиномиальную интерполяцию по заданным векторам X и Y размерности N в точке x. Она находит полином степени N-1, проходящий через каждую точку {Xi,Yi}. Функция возвращает вектор, состоящий из 2 элементов - найденное в точке x значение полинома и оценка погрешности значения.
Проиллюстрируем работу функции, задав векторы X и Y "вручную", а для оценки значения полинома определив точку x=25.
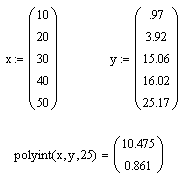
Функция polycoeff(X,Y) вычисляет коэффиценты интерполяционного полинома и возвращает вектор этих коэффициентов размерностью N для N значений {Xi,Yi}. В дальнейшем в произвольной точке x значение интерполяционного полинома может быть вычислено по формуле f(x)=Σcixi
Ниже вычисляется значение полинома и его первой производной для тех же векторов исходных данных X, Y и той же точки x=25.
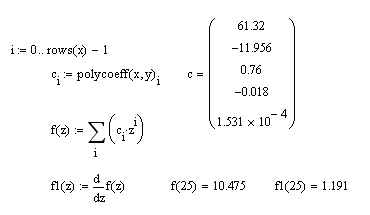
Функция polyiter(X,Y,x,N,e) позволяет задать значение допустимой погрешности e и максимальную степень полинома N, таким образом, с её помощью можно выполнять полиномиальную интерполяцию более низких степеней. Проверим её работу на степени N-1.
Более развёрнутый пример с графиками - в приложенном файле MathCAD (формат .XMCD)
![]() Скачать этот пример в формате XMCD (105 Кб)
Скачать этот пример в формате XMCD (105 Кб)
| Ещё одна простая и "ручная" реализация интерполяционного полинома + просто о теории |
Интерполяционный полином
Во многих случаях анализируемые данные заданы не аналитическим способом (в виде известной функции y(x)), а табличным – когда значения функции известны только для конечного набора значений аргументов yi=f(xi), i=1,2,…,N. При этом аналитическая формула для функции f(xi) нам неизвестна, так что мы не можем достоверно оценить её значение в какой-либо точке кроме тех, что нам известны. Восстановить зависимость по N известным точкам можно из следующих соображений.
Через N различных точек {xi,yi}, i=1,2,…,N, всегда можно построить кривую, зависящую от xN-1:
• прямая может быть построена по 2 точкам (уравнение зависит от x1 и имеет вид f(x)=c0+c1*x);
• парабола может быть построена по 3 точкам (уравнение зависит от x2 и имеет вид f(x)=c0+c1*x+c2*x2);
• …
• в общем виде для N точек уравнение имеет вид f(x)=c0+c1*x+c2*x2+…+сN-1*xN-1 и зависит от xN-1
(формула 1)
В этом уравнении нам неизвестны коэффициенты ci. Из условия, что кривая проходит через все известные точки, можно записать:
|
|
c0 + c1x1 + c2x12
+ …. + cN-1x1N-1 = y1
c0 + c1x2 + c2x22 + …. + cN-1x2N-1 = y2 … c0 + c1xN + c2xN2 + …. + cN-1xNN-1 = yN
|
или в матричном виде |  | * |  | = | 
|
Решив эту систему уравнений, то есть, найдя обратную матрицу и умножив её на вектор y, найдём коэффициенты ci. Подставив их в уравнение (1), мы можем аналитически оценить значение функции в любой точке x. Построенная по формуле (1) кривая называется интерполяционным полиномом.
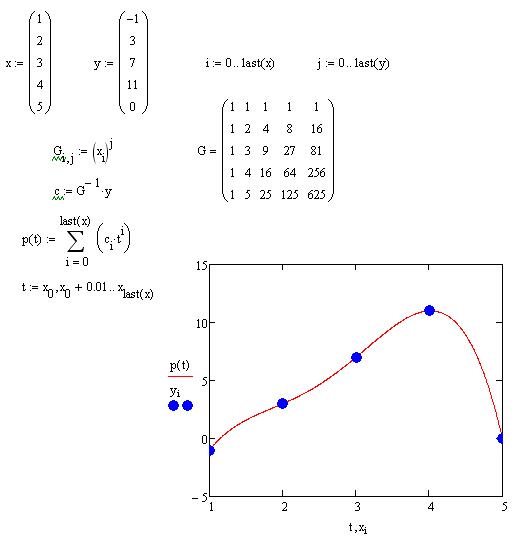
Задание: построить интерполяционный полином по следующим значениям {xi,yi}:
|
i |
1 |
2 |
3 |
4 |
5 |
|
xi |
1.5 |
2.5 |
4 |
5.5 |
7 |
|
yi |
-1 |
3 |
7 |
11 |
0 |
Вывести на графике полученную зависимость f(x) и исходные данные {xi,yi}, границы графика по оси Ox принять от 0 до 5.
Скриншот:
![]() Скачать этот пример в формате XMCD (35 Кб)
Скачать этот пример в формате XMCD (35 Кб)
|
|