Теорию можно почитать, например, здесь (раздел "Глобальная интерполяция").

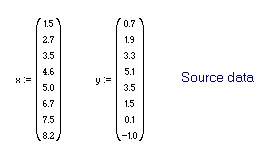
Исходные данные для расчёта заданы двумя векторами произвольной размерности - X и Y. Разумеется, размерность векторов одинакова (обозначим её N).

Строим матрицу коэффициентов полинома (матрицу Вандермонда) размерностью N*N.

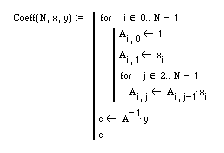
После вызова только что показанной функции, используем найденный ею вектор коэффициентов глобального полинома c для поиска значений в ранее заданных точках xi.

Значения совпали с заданными yi - значит всё правильно, полином-то интерполяционный и должен проходить через все точки.

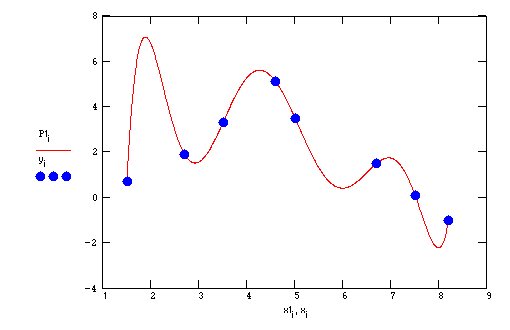
Можно сделать произвольный дискретный диапазон по x и рассчитывать полином Лагранжа в произвольной точке, вызывая функцию P(c,x). Для простоты возьмём интервал, совпадающий с минимальным и макисмальным значениями из заданных иксов - то есть, от 1.5 до 8.2 и разобъём его на N участков.

Видно, что в промежуточных точках значения полинома другие. Итак, по набору из N заданных точек (xi,yi) мы построили кривую, завиящую от xN-1 и проходящую через все точки. Что получилось и этот пример для скачивания - ниже.

 Канонический интерполяционный полином в MathCAD, пример (11 Кб)

гостевая; E-mail