Выпуклый четырёхугольник задан координатами своих вершин A, B, C, D в порядке их обхода. Проверить, является ли четырёхугольник ромбом или квадратом, выдать соответствующее сообщение.

Здесь мы расположим X- и Y-координаты вершин в массивах X и Y соответственно, а затем посчитаем стороны и диагонали четырёхугольника, записывая эту информацию в массив R.

Следует помнить о возможной погрешности при сравнении вещественных чисел, так что в профессиональной программе условие r[i]<>r[4] следовало бы заменить чем-то вроде abs(r[i]-r[4])<eps, где eps - допустимая погрешность.

function dist (x1,y1,x2,y2:real):real;
{Расстояние между точками (x1,y1), (x2,y2)}
begin
 dist:=sqrt(sqr(x1-x2)+sqr(y1-y2));
end;

var x,y:array [1..4] of real;
 r:array [1..6] of real;
 i,k:integer;

begin
 for i:=1 to 4 do begin
  write ('Введите координаты ',i,' точки:');
  read (x[i],y[i]);
 end;
 r[4]:=dist(x[1],y[1],x[4],y[4]);
 k:=0;
 for i:=1 to 3 do begin
  r[i]:=dist(x[i],y[i],x[i+1],y[i+1]);
  if r[i]<>r[4] then k:=1;
 end;
 if k=0 then begin
  r[5]:=dist(x[1],y[1],x[3],y[3]);
  r[6]:=dist(x[2],y[2],x[4],y[4]);
  if r[5]=r[6] then writeln ('Квадрат')
  else writeln ('Ромб');
 end
 else writeln ('Не ромб и не квадрат');
 reset (input); readln;
end.

Что изменится, если точки перечислены не в порядке обхода? Как минимум, нужно отсортировать их так, чтоб стали в порядке :) Также следует предварительно избавиться от возможных повторяющихся значений точек.

Разовьём задачу. Что делать, если нужно проверить, какие из набора точек образуют квадраты на плоскости? Приходит в голову такой алгоритм. Предположим, что точки никак не упорядочены, но различны между собой и количество их - не менее четырёх. Переберём все возможные разбиения точек по 4 элемента. Для того чтобы проверить, лежат ли 4 точки в вершинах прямоугольника, переберём все перестановки последних трёх точек и проверим, что каждые 2 последовательных отрезка, соединяющих последовательные точки, образуют прямой угол. Это можно сделать используя то, что скалярное произведение двух векторов равно нулю тогда и только тогда, когда угол между ними - прямой.

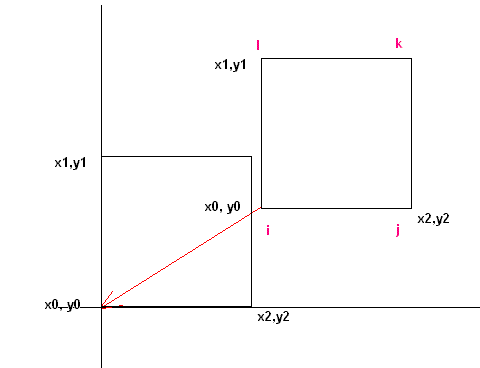
В нашем случае скалярное произведение можно найти также по формуле x1*x2+y1*y2, где вектора (x1,y1), (x2,y2) получены переносом в точку (x0,y0) начала координат (см. рис. и функцию angle)

Для проверки того, лежат ли 4 точки в вершинах квадрата, а не просто прямоугольника, дополнительно нужно проверить, что 2 соседние стороны равны. Приведём листинг на Паскале:

{Предполагается что задано не менее 4 точек и все они различны}
uses crt;
type point = array [1..2] of real;
const n=11;
 p:array [1..n] of point = (
  (8,8), (0,8), (8,0), (1,2),
  (0,0), (4,4), (4,0), (0,4),
  (2,3), (3,2), (2,1)
 );

function dist (i,j:integer):real;
begin
 dist:=sqrt(sqr(p[i,1]-p[j,1])+sqr(p[i,2]-p[j,2]));
end;

function angle (i,j,k:integer):boolean;
var p0,p1,p2:point; s:real;
begin
 p0:=p[i]; p1:=p[j]; p2:=p[k];
 p1[1]:=p1[1]-p0[1]; p1[2]:=p1[2]-p0[2];
 p2[1]:=p2[1]-p0[1]; p2[2]:=p2[2]-p0[2];
 s:=p1[1]*p2[1]+p1[2]*p2[2];
 if s=0 then angle:=true
 else angle:=false;
end;

function square0 (i,j,k,l:integer):boolean;
begin
 if (angle(i,l,j)=true) and
    (angle(k,j,l)=true) and
    (dist(i,l)=dist(i,j)) and
    (dist(i,j)=dist(j,k)) then square0:=true
 else square0:=false;
end;

function square (i,j,k,l:integer):boolean;
begin
 if (square0(i,j,k,l)=true) or
    (square0(i,j,l,k)=true) or
    (square0(i,k,j,l)=true) or
    (square0(i,k,l,j)=true) or
    (square0(i,l,j,k)=true) or
    (square0(i,l,k,j)=true) then square:=true
 else square:=false;
end;

var i,j,k,l:integer;

begin
 clrscr;
 for i:=1 to n-3 do
 for j:=i+1 to n-2 do
 for k:=i+2 to n-1 do
 for l:=i+3 to n do
  if square(i,j,k,l)=true then writeln (
   '(',p[i,1]:2:0,',',p[i,2]:2:0,'), ',
   '(',p[j,1]:2:0,',',p[j,2]:2:0,'), ',
   '(',p[k,1]:2:0,',',p[k,2]:2:0,'), ',
   '(',p[l,1]:2:0,',',p[l,2]:2:0,')');
end.

"Лишние" вызовы функции dist из square0 нужны здесь затем, чтобы не выводить несколько раз квадраты, отличающиеся лишь порядком образующих их точек - ведь последние 3 точки переставляются (за счёт перестановок индексов j, k, l в коде).

Есть ещё такой вариант решения - если окружность вписана в квадрат то она касается всех его сторон посредине, а её радиус равен половине стороны. То есть, мы могли бы искать середины всех сторон и рассчитывать предполагаемое место для центра окружности. Если все 4 отрезка от центра до каждой из середин сторон равны, то наш четырехугольник - квадрат.

гостевая; E-mail