Заданы координаты N различных между собой точек на плоскости, поместим их в матрицу A размерностью Nx2. Во многих задачах уже предполагается, что точки уже перечислены в порядке их обхода по часовой стрелке (или против неё), например, если эти точки образуют многоугольник. На самом деле точки могут вводиться пользователем (или ещё откуда-то читаться) в любом порядке, и зачастую нам нужно, как минимум, упорядочить точки так, чтобы через них можно было провести несамопересекающуюся ломаную (а ещё лучше - построить простой многоугольник).

Так, программа "Ромб или квадрат", не поймёт, что точки (0,0), (1,1), (1,0), (0,1) образуют квадрат, если мы перечислим их именно в таком порядке, правильно, например, (0,0), (1,0), (1,1), (0,1).

Простой алгоритм для описанного упорядочения найти не так уже легко. Предлагается следующее решение:

• Находим самую нижнюю (минимальную по Y) точку, если таковых несколько - берём ту, что имеет большую координату по X, то есть, правую точку. Записываем эту точку как A[1].
• Все остальные точки сортируем по возрастанию угла относительно A[1], если у каких-то точек есть одинаковый угол - то по расстоянию от A[1].
• Получившиеся точки образуют ломаную без самопересечений, давая нам тот самый "естественный порядок обхода".

Вычислить угол между векторами можно по формуле

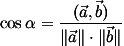
то есть, косинус угла между векторами на плоскости равен скалярному произведению векторов, делённому на произведение их длин.

const n=5; {Количество точек}
type point = array [1..2] of real; {Тип данных "точка"}
     points=array [1..n] of point; {Массив точек задачи}
var a:points;

procedure gen (var a:points);
{Сгенерировать точки - координаты берем целые от -10 до 10}
var i:integer;
begin randomize;
 for i:=1 to n do begin
  a[i,1]:=round(random*20-10);
  a[i,2]:=round(random*20-10);
 end;
end;

function scal (a,b:point):real;
{Скалярное произведение 2 векторов на плоскости}
begin scal:=a[1]*b[1]+a[2]*b[2]; end;

function len (a:point):real;
{Длина вектора на плоскости}
begin len:=sqrt(sqr(a[1])+sqr(a[2])); end;

procedure swap (var a,b:point); {Обменять значения 2 точек}
var c:point;
begin
 c:=a; a:=b; b:=c;
end;

procedure sort (var a:points); {Основная процедура}
var ymin,xmax,ks:real;
 i,imin,k,j:integer;
 b:array [1..n] of integer;
 u:array [1..n] of real;
begin
 ymin:=1e30;
 for i:=1 to n do if a[i,2]<ymin then begin ymin:=a[i,2]; imin:=i; end;
 k:=0; {В худшем случае все точки одинаковы по ординате}
 for i:=1 to n do if a[i,2]=ymin then begin inc(k); b[k]:=i; end;
 if k<1 then begin writeln ('Не найдено самой нижней точки!'); exit; end;
 xmax:=a[b[1],1];
 if k>1 then for i:=2 to k do if a[b[i],1]>xmax then begin
  xmax:=a[b[i],1]; imin:=b[i];
 end;
 {Номер нужной точки в imin}
 swap (a[1],a[imin]);
 u[1]:=0;
 for i:=2 to n do begin {Вычисляем косинусы и углы}
  ks:=scal(a[1],a[i])/(len(a[1])*len(a[i]));
  if ks=0 then u[i]:=90
  else if ks>0 then u[i]:=arctan(sqrt(1-sqr(ks))/ks)*180/pi
  else u[i]:=180+arctan(sqrt(1-sqr(ks))/ks)*180/pi;
 end;
 {Сортируем по углам, одинаковые углы - по убыванию длины вектора}
 for i:=1 to n-1 do
 for j:=i+1 to n do
 if (u[i]>u[j]) or (u[i]=u[j]) and (len(a[i])<len(a[j])) then begin
  ks:=u[i]; u[i]:=u[j]; u[j]:=ks;
  swap(a[i],a[j]);
 end;
end;

procedure out (a:points); {Вывести точки}
var i:integer;
begin
 for i:=1 to n do write ('(',a[i,1]:5:2,',',a[i,2]:5:2,')  ');
 writeln;
end;

begin
 gen(a);
 {Ниже - закомментаренный блок для тестов}
 {
 a[1,1]:=1; a[1,2]:=0;
 a[2,1]:=2; a[2,2]:=0;
 a[3,1]:=3; a[3,2]:=0;
 a[4,1]:=4; a[4,2]:=0;
 a[5,1]:=5; a[5,2]:=0;
 }
 writeln ('Сгенерированы точки');
 out (a);
 sort(a);
 writeln ('Получены точки');
 out (a);
 write ('ENTER для выхода');
 reset (input); readln;
end.

Немаловажный нюанс - имеет смысл понятие угла только между двумя ненулевыми векторами, если хотя бы один из них равен нулю, то возникает деление на ноль при вычислении косинуса угла.

Нигде в литературе не оговаривается сонаправленность нулевого вектора и какого-либо другого, так что если в расчётах есть точка (0,0), сдвиньте систему координат, например, прибавив (отняв) по единице ко всем значениям x. Разумеется, при этом нужно следить, чтоб не появилось новой точки (0,0) :)

Непосредственно этот алгоритм не подойдёт и для сортировки вершин выпуклого многоугольника в порядке обхода, для этого есть гораздо более мощные (и сложные в реализации) алгоритмы Грэхема, Gift Wrapping и другие. Так, для нашего квадратика точки (1,0), (2,1), (1,1), (2,0) дадут на выходе порядок (2,0), (1,0), (2,1), (1,1), что неверно.

гостевая; E-mail