В детстве я жалел составителей логарифмических таблиц - их работа казалась мне эталоном бесполезности, ведь о "построении в России демократического общества" я тогда ещё ничего не знал. Не знал я и более важных вещей, например, того, что закономерное лучше всего познаётся через достаточно длинные цепочки случайностей, хоть в математике, хоть в обычной жизни. Одна из основных проблем, мешающих математическим обобщениям, как раз то, что цепочки "чисто случайных" чисел недостижимы (любой генератор выдаёт только псевдослучайные числа), а с другой стороны, все закономерности выполняются лишь статистически и приблизительно, так что "чистая закономерность" тоже возможна лишь на бумаге.

Приведём один пример, раз уж он мне попался на компьютере, а до следующей рабочей встречи ещё час.

Взять определённый интеграл в MathCAD - одна из самых простых задач, о которых я слышал. Нажимаем в программе символ "&", а дальше можно догадаться...

Но мы лёгких путей не ищем, тем более, что практически все трудоёмкие расчёты можно приблизительно выполнить на основе последовательностей псевдослучайных чисел - были бы достаточно длинными их серии.

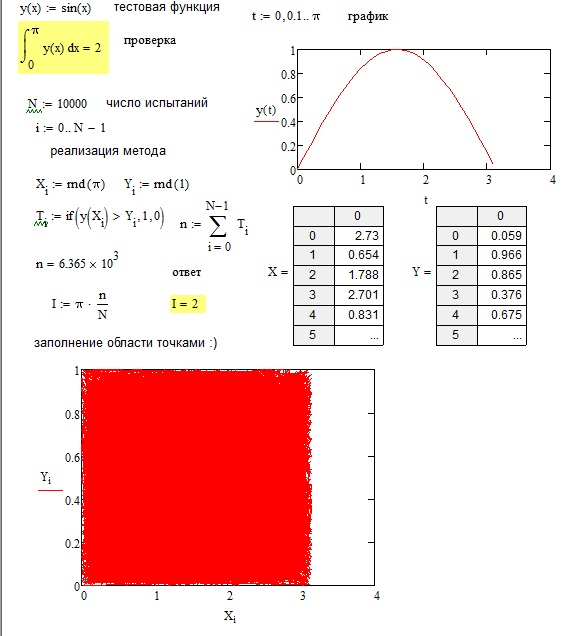
Основная идея метода Монте-Карло в применении к интегрированию очень проста - вписать график функции в прямоугольник, потом бросать на прямоугольную область, в которую вписан график, случайные "камешки".

Поскольку для примера мы взяли синусоиду и интервал интегрирования от 0 до π, площадь нашего прямоугольника тоже равна π (максимум синуса на этом интервале равен 1).

Отношение числа n попаданий "камешка" под график к общему числу "камешков" N даст значение определённого интеграла :) Просто умножим эту величину на площадь прямоугольника, получая формулу I=π*n/N.

В общем случае нужно заменить в формуле π на площадь прямоугольника, который занимает функция.

Как Вы понимаете, делать такое для обычной синусоиды бессмысленно, благо, кроме всеми забытой аналитической математики, существуют и удобные (для компьютеров) численные методы, но представьте, что нужно численно оценить площадь объекта с действительно сложной формой, а никакого уравнения, описывающего контур объекта, у нас нет... зато мы можем отличить попадание точки "внутрь" объекта от попадания её "снаружи" - пусть даже по цвету пиксела на фото. В таких задачах наше стохастическое интегрирование может оказаться незаменимым.

В прилагаемом документе всё сделано удобней, чем на скрине (есть поля для ввода пределов интегрирования a, b, автоматически проводится исследование функции на максиммум в интервале x∈[a,b], лучше визуализация). В целях совместимости файл сохранён в формате MathCAD 11, значит, открывается в любой старшей версии.

 Интегрирование методом Монте-Карло в MathCAD (11 Кб)

Кстати, если Ваш MathCAD показывает вместо русских шрифтов "козяблики" - а этим грешат все версии от 10 до 14 - то либо поменяйте шрифт текстовых надписей на любой, имеющий в окончании названия Cyr (не Times New Roman, а Times New Roman Cyr), либо выполните на компьютере такой же патчик, как в этой заметке блога.

гостевая; E-mail