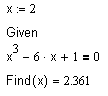
|
Pers.narod.ru. Обучение. 3 способа решения уравнений в MаthCAD |
В MathCAD есть все возможности как для численного, так и для аналитического (символьного) решения уравнений. Притом, что пользоваться этими возможностями очень легко.
1. Уравнение можно решить с помощью блока Given - Find. Поскольку у сложного нелинейного уравнения может быть множество решений, нужно задать начальное значение неизвестной переменной, входящей в уравнение. Тогда будет найден ближайший к этому начальному значению корень.
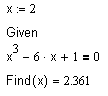
Обратите внимание, что в записи уравнения левая часть отделена от правой жирным знаком = (логическим равенством). Он вводится комбинацией клавиш Ctrl+=.
Систему уравнений, в том числе, нелинейных, решить ничуть не сложнее:
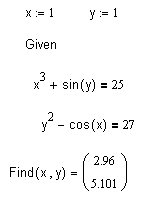
Кстати говоря, уравнение вообще не обязано иметь решений. Но его всё равно можно "решить" блоком Given-Minerr вместо Given-Find!
Просто если решения нет, блоком Given-Minerr будет найдена минимальная невязка уравнения, т.е., значение x, при котором левая и правая части уравнения наиболее близки.

2. Уравнение можно также решить с помощью стандартной функции root. В качестве параметров методу
root нужно указать левую часть уравнения f(x)=0, переменную, которая является аргументом (например, x) и интервал поиска корня. На концах этого интервала функция f(x) должна иметь разные знаки, тогда будет найден корень уравнения. В противном случае стоит ожидать сообщения об ошибке.
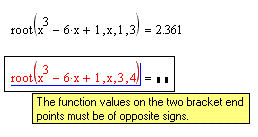
Если, как в первом способе, задать начальное значение аргумента, то можно обойтись и без указания интервала:
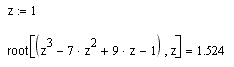
3. Если, как это часто бывает, уравнение может быть записано в виде многочлена некоторой степени от одной переменной (как всегда, обозначим её x), мы можем просто "загнать" в вектор коэффициенты при степенях x, начиная с нулевой, и затем вызвать функцию polyroots, которая найдёт все корни многочлена и вернёт их в виде вектора.
Так, для нашего уравнения x3-6x+1=0 получится вот что:

![]() Скачать этот пример в формате MCD (9 Кб)
Скачать этот пример в формате MCD (9 Кб)
О решении уравнений в символьной форме можно посмотреть, например, в этом архиве (работа 5).
|
|