На практике чаще всего мы имеем дело с одним из трёх видов распределений случайной величины:

Описание распределения	Вид функции плотности вероятности
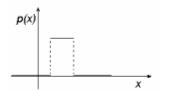
Равномерное: возникает, если случайная величина принимает конечное число значений с равными вероятностями... ну или примерно равными :)
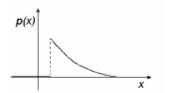
Экспоненциальное (показательное): хорошо моделирует интервалы времени между двумя последовательными свершениями одного и того же события... ну или всякие схемы редких событий, если привлечь связанное с ним обратной зависимостью дискретное распределение Пуассона
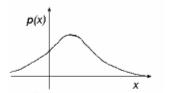
Нормальное: самое популярное в природе распределение, проявляется практически всегда, когда случайная величина является результатом действия большого количества различных факторов. К тому же, к нормальному распределению сходятся при большом числе испытаний (или иначе связаны с ним) почти все остальные рассматриваемые отдельно распределения (биномиальное, хи-квадрат, Стьюдента, Фишера и т.д.)

Приложенные ниже 3 документа позволяют "посмотреть в действии" нормальное, показательное и равномерное распределения - в каждом документе моделируются по N=10000 испытаний (значение N можно изменить), вычисляются выборочные и теоретические параметры распределения, вероятности того, что случайная величина примет значение, принадлежащее заданному интервалу, аналитически и графически строятся функции распределения и плотности вероятности.

Скриншот части одного из документов:

 Равномерное распределение в MathCAD (документ .xmcd) (74 Кб)

 Показательное (экспоненциальное) распределение в MathCAD (документ .xmcd) (60 Кб)

 Нормальное распределение в MathCAD (документ .xmcd) (68 Кб)

гостевая; E-mail