Програмирование в пакете MathCAD

Существуют два способа программирования в MathCAD:

·        программирование в пакете MathCAD без использования программных модулей;

·        программирование с использованием программных модулей.

Первый способ (в дальнейшем для простоты названный безмодельным программированием) реализуется записью соответствующих конструкций непосредственно в математических областях документа MathCAD, и он приемлем для сравнительно простых алгоритмов.

Второй способ (называемый для простоты модульным программированием) предполагает реализацию отдельных независимых алгоритмов вычисления (например, решение нелинейного уравнения методом «деления отрезка пополам») в виде отдельных программных модулей, которые будем называть программами-функциями (сокращенно П-Ф).

БЕЗМОДУЛЬНОЕ ПРОГРАММИРОВАНИЕ В ПАКЕТЕ MathCAD

Программирование линейных алгоритмов

Характерной особенностью линейных алгоритмов является строго последовательное выполнение всех операций алгоритма без пропусков и повторений вычислений. Поэтому конструкции, реализующие такой алгоритм, записываются в документе MathCAD в нужном порядке их выполнения, т.е. «слева-направо  –  сверху-вниз».

Пример 1.          Составить программу для вычисления корней квадратного уравнения:  ax² + bx + c = 0  по известной формуле:

               (1)

Алгоритм (1) является линейным и фрагмент документа MathCAD содержит конструкции, приведенные на рис 1.

Программирование разветвляющихся алгоритмов

Характерной чертой разветвляющихся алгоритмов является наличие в них нескольких возможных ветвей вычислений. Выбор конкретной ветви зависит от выполнения (или не выполнения) заданных условий на значения переменных алгоритма.

           Пример 2. Значение переменной y зависит от значений переменной x и определяется выражением:

Для реализации разветвляющегося алгоритма необходимо использовать:

·        конструкции, проверяющие выполнение  заданных условий;

·        конструкции, выбирающие нужную ветвь вычислений в зависимости от результатов проверки заданных условий.

Для проверки заданных условий  в MathCAD используется: выражение отношений,  логические операции и логические выражения.

Выражением отношений (или просто отношением) называется конструкция вида:

<выр.1> <операция отношения> <выр.2>,

где    <выр.1>,  <выр.2> - произвольные арифметические выражения, <операция отношения> - любая из следующих операций:  (здесь вертикальные чёрточки являются разделительным символом при перечислении).

Для ввода знаков операций отношений  можно использовать палитру  Булево (приведённую на рис.3) или использовать клавиши, обозначения которых приведены в таб. 1.

Палитра инструментов  БУЛЕВО

    Внимание! Не следует путать знак операции сравнения = с похожим знаком вывода значений переменных. Знак операции = имеет больший размер и более жирное начертание.

Таблица 1

Выражение отношений принимает одно из двух значений: 1 - если заданное отношение выполняется или  0 – в противном случае. Значение  1 можно интегрировать как значение истина, а 0 – как ложь.

Задание  1.  Пусть значения целой переменной  x =3. Определить значение следующих выражений    отношений:

 Для проверки более сложных условий используются четыре логических операций, обозначение которых приведены в табл. 2

Таблица 2

Знаки этих операций  вводится с палитры Булево. Результат выполнения этих операций, приведен в табл. 3.

Таблица 3

Логическим выражением называется конструкция, состоящая из выражений отношений, логических операций  и  круглых скобок. Логическое выражение принимает только одно из двух значений: 1 или 0; вычисляется слева направо с учетом приоритета входящих в выражение операции. Наивысший приоритет круглые скобки, а затем по убыванию: AND, OR и XOR – одинаковый приоритет и самый низкий приоритет выражения отношений.                       

Задание 2. Определите порядок вычисления значений логических выражений в документе MathCAD, приведенных на рисунке 3

      Рис. 3 Примеры логических выражений

Пример 2.  Записать логическое выражение, принимающее значение 1 при попадании точки с координатами (x, y) в первую четверть.

Логическое выражение имеет вид

Для выбора нужной ветви разветвляющегося алгоритма используется конструкция, названная условной функцией if,  записывается в виде:

if (<логическое выражение>, <выр. 1>, <выр. 2>),

где имя функции if вводится с клавиатуры.

Если логическое выражение равно 1, то значение функции определяется выр.1, в противном случае – выр. 2.  Блок-схема этой функции приведена на рис. 4.

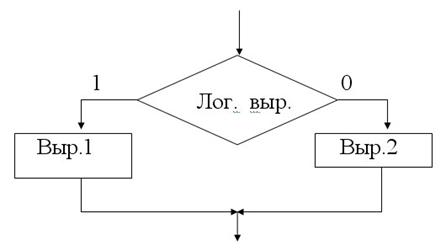
Рис. 4.  Блок-схема функции  if

При программировании разветвляющихся алгоритмов с тремя и более вычислительных ветвей на месте выр. 1 и выр. 2 вновь может использоваться функция if .

Пример 3. Используя условную функцию if запрограммировать два разветвляющихся алгоритма:

а)        

б)         

Рис. 5. Реализация разветвляющихся алгоритмов

В MathCAD имеется ряд встроенных функций, которые возвращают результат, зависящий от знака или величины аргумента и которые могут использоваться при программировании разветвляющихся алгоритмов. Приведем некоторые из них:

·        ceil (x) – наименьшее целое, большее или равное x;

·        trunc (x) – целая часть вещественного числа x;

·        floor (x) – наибольшее целое, меньшее или равное x;

·        round (x, n) – округленное значение вещественного x с точностью до n знаков после десятичной точки;

·        Ф(x) – функция Хевисайда – равна 0 при  x < 0  и 1 в противном случае;

·        sign (x) – функция знака (равна 0 если x = 0; -1, если x <0 и   1, если  x >0);

·        signum (x) – возвращает 1, если x = 0 и  в остальных  случаях.

Программирование циклических алгоритмов

Типы циклов. По способам организации цикла можно выделить:

а) цикл типа арифметической прогрессии;

б) итерационный цикл.

Программирование цикла типа арифметической прогрессии

Особенностью цикла типа арифметической прогрессии является изменение параметра цикла по закону арифметической прогрессии и поэтому можно, не выполняя цикла, определить количество повторений цикла.

 Параметр такого цикла задается дискретной переменной и тогда конструкции, входящие в тело цикла располагаются, начиная от этого описания и до конца документа MathCAD или до конструкции, переопределяющей дискретную переменную – параметр цикла.

Этот цикл имеет уже два параметра: i – параметр, определяющий номер строки;  j – параметр, определяющий номер столбца матрицы. Заметим, что такой цикл называется двойным циклом.

Заметим, что если параметр цикла не входит в индексные выражения элементов массива, то он может принимать вещественные значения.

            Заметим, что во фрагментах, приведенных на рисунках системная переменная ORIGIN=1.

гостевая; E-mail