
|
Pers.narod.ru. Обучение. Лекции по MathCAD. 3. Массивы в MathCAD |
Массивы в Mathcad
Столбец чисел называется вектором, а прямоугольная таблица чисел - матрицей. Общий термин для вектора или матрицы - массив. При работе с матрицами используется панель инструментов “Матрицы”:

Обращение к элементам массива
Обращение к элементу массива осуществляется путем записи имени массива и соответствующих индексных выражений, количество которых определяется размерностью массива.
Для ввода индексных выражений обязательно нажать клавишу [ [ ] – левую квадратную скобку. При этом курсор перемещается вниз, и индексные выражения оказываются смещенными относительно имени массива.
Внимание! После завершение ввода индексных выражений обязательно охватить выделяющим уголком имя и индексные выражения массива.
Внимание! Смещение
вниз вызывает также нажатие клавиши ![]() , но она используется только для ввода
нижних индексов в имени переменной, но не индексных выражений.
, но она используется только для ввода
нижних индексов в имени переменной, но не индексных выражений.
На
рисунке показан фрагмент присваивания значений отдельным элементам массивов:
векторов ![]() и
матриц
и
матриц ![]() . Здесь
же приведен вывод этих массивов.
. Здесь
же приведен вывод этих массивов.
Начальное
значение индексных выражений определяется системной переменной ![]() и по умолчанию ее
значение равно 0.
и по умолчанию ее
значение равно 0.
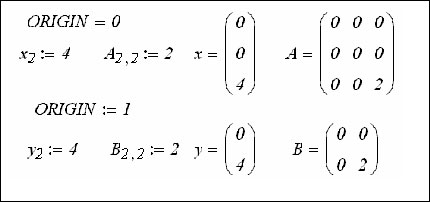
Для
перехода к привычной нумерации (с начального значения 1) необходимо изменить
значение системной переменной ![]() .
.
Это можно осуществить двумя способами:
а) задать в документе новое значение с помощью оператора присваивания (область действия нового значения – весь ниже лежащий документ);
б) обратиться к пункту меню Математика команда Опции и в появившемся диалоговом окне изменить значение опции Исходное множество на нужное значение (например, 1).
Верхний индекс матрицы
Верхний индекс – позволяет обратиться к отдельному столбцу массива.
Чтобы вставить верхний индекс, введите имя массива, а затем нажать клавиши
[Ctrl + 6]
или нажать на кнопку ![]() :
:
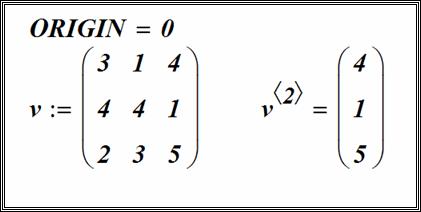
![]()
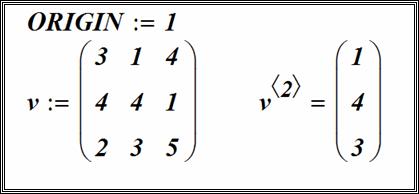
Создание вектора и матрицы
Способ 1. Заполнение шаблона.
· введите имя матрицы и знак присваивания (двоеточие)
·
щелкните по значку ![]() в
панели “Матрицы”. В появившейся диалоговой панели введите число строк и
столбцов матрицы.
в
панели “Матрицы”. В появившейся диалоговой панели введите число строк и
столбцов матрицы.
· После нажатия кнопки OK открывается поле для ввода элементов матрицы. Заполните метки - заполнители соответствующими значениями.
Примеры определения векторов и матриц:
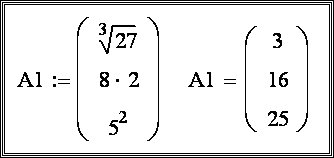
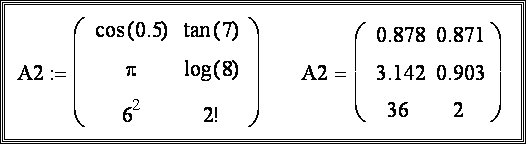
Способ 2. Ввод с клавиатуры в цикле
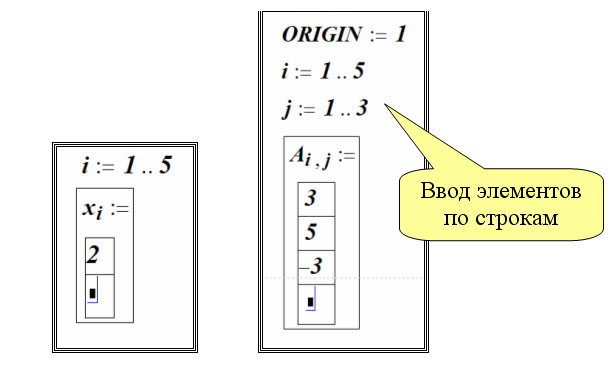
Способ 3. Формирование элементов по заданному выражению.
Сформировать вектор по правилу ![]() и матрицу D размером
и матрицу D размером ![]() по правилу
по правилу 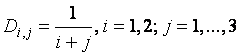 .
.
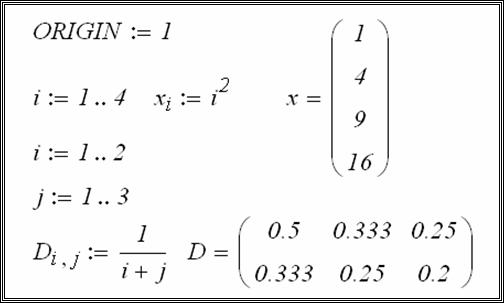

Изменение размера матрицы
Можно изменять размер матрицы, вставляя и удаляя строки и столбцы. Для этого необходимо выполнить следующее:
· Щёлкните на одном из элементов матрицы, чтобы заключить его в выделяющую рамку.
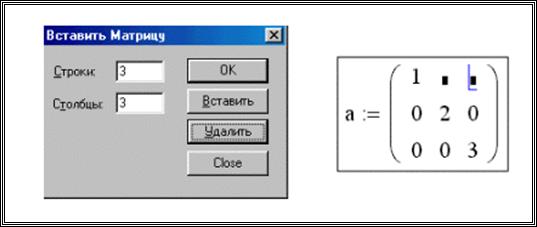
· Щелкните по значку “создать матрицу” в панели “Матрицы. Появляется диалоговое окно.
· Напечатайте число строк и (или) столбцов, которые нужно вставить или удалить. Затем нажмите на “Вставить” или на “Удалить”.
Например, чтобы удалить 1-й столбец, выделите элемент столбца (число 2), вызовите диалоговое окно “создать матрицу”, напечатайте 1 в поле “Столбцов”, 0 в поле “Строк”, и нажмите на “Удалить”.


Рассмотрим различные ситуации удаления или вставки строк или столбцов:
· Если вставляются строки, Mathcad создает строки пустых полей ниже выбранного элемента. Если вставляются столбцы, Mathcad создает столбцы пустых полей справа от выбранного элемента.
· Чтобы вставить строку выше верхней строки или столбец слева от первого столбца, сначала заключите матрицу целиком в выделяющую рамку, щёлкнув внутри и нажав клавишу пробел несколько раз. Затем щелкните по значку “создать матрицу” и продолжите, как обычно.
· Когда удаляются строки или столбцы, Mathcad удаляет строки вниз от этого элемента, а столбцы — направо от этого элемента.
Внимание!!! При удалении строк или столбцов Mathcad удаляет содержащуюся в них информацию.
Операции над векторами

Операции над матрицами





Функции для обработки значений массива можно
вводить, используя Мастера функций (для вызова щелкнуть на значке ![]() )
)


Функции размера и диапазона значений массива
В Mathcad есть несколько функций, которые возвращают информацию относительно размеров массива и диапазона его элементов:
· rows(A) – число строк в массиве A.
· cols(A) – число столбцов в массиве A.
· length(v) – число элементов в векторе v.
· last(v) – индекс последнего элемента в векторе v.
· max(A) – определяет cамый большой элемент в массиве A; если A имеет комплексные элементы, то возвращает наибольшую вещественную часть плюс i, умноженную на наибольшую мнимую часть.
· min(A) – определяет cамый маленький элемент в массиве A; если A имеет комплексные элементы, то возвращает наименьшую вещественную часть плюс i, умноженную на наименьшую мнимую часть.
Функции формирование специального типа матриц
· identity(n) – формирует n x n единичную матрицу (матрица, все диагональные элементы которой равны 1, а все остальные элементы равны 0).

· geninv(A) – формирует левую обратную к A матрицу L такую, что L∙A = I, где I - единичная матрица, имеющая то же самое число столбцов, что и A. Матрица А - m x n вещественная матрица, где m>=n.

· Re(A) – формирует массив, состоящий из элементов, которые являются вещественными частями элементов A.
· Im(A) – формирует массив, состоящий из элементов, которые являются мнимыми частями элементов A.
· diag(v) – формирует диагональную матрицу, содержащую на диагонали элементы вектора v.

· matrix(m,n,f) – создает и заполняет матрицу размером m x n, элемент которой, расположенный в строке i и столбце j, равен f(i,j).

Функции формирование новых массивов из существующих
· augment (A, B) - формирует массив, расположением A и B бок о бок, причем массивы A и B должны иметь одинаковое число строк.
· stack (A, B) - формирует массив, расположением A над B , причем массивы A и B должны иметь одинаковое число столбцов.
· submatrix (A, ir, jr, ic, jc) - формирует подматрицу, содержащую строки с ir по jr и столбцы с ic по jc матрицы A.



Специальные характеристики матрицы
· tr(M) – вычисляет сумму диагональных элементов, называемых следом M.
· rank(A) – возвращает ранг вещественной матрицы A.
· norm1(M) – вычисляет L1 норму матрицы M.
· norm2(M) – вычисляет L2 норму матрицы M.
· normi(M) – вычисляет равномерную норму матрицы M.
· norme(M) – вычисляет евклидову норму матрицы M.
· cond1(M) – вычисляет число обусловленности матрицы M, основанное на L1 норме.
· cond2(M) – вычисляет число обусловленности матрицы M, основанное на L2 норме.
· conde(M) – вычисляет число обусловленности матрицы M, основанное на евклидовой норме.
· condi(M) – вычисляет число обусловленности матрицы M, основанное на равномерной норме.

Задание
1. Вычислите матрицу 2*A*B-3*C*D, где:


2. Вычислите матрицу F = A*(2B-3*C)-D
3. Найдите определитель и обратную матрицу для матриц:

4. Вычислите матричные выражения:

5. Получите матрицу С перестановкой 2-го и 3-го столбцов матрицы A
6. Решите систему линейных уравнений A*x=b, где
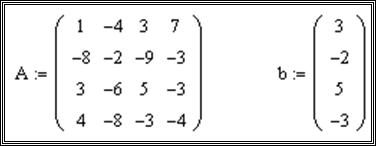
Вектор x вычисляется как x=A-1*b.
7. Выясните, являются ли линейно-независимыми векторы p,q,r:

(Напоминаем, что векторы линейно независимы, если смешанное
произведение  равно нулю)
равно нулю)
|
|