Я настолько давно и прочно привык делать всё, что можно сделать в Excel, "Поиском решения", что удивляюсь, когда кто-то так не делает. Поэтому добавлю несколько слов об этом полезном инструменте и приведу какой-нибудь пример.

В общем виде задача оптимизации ставится следующим образом: найти максимальное, минимальное или фиксированное значение функции f(x1,x2,…,xn) при заданной системе ограничений ai ≤ xi ≤ bi , i=1,2,…,n, где xi – неизвестные величины. В реальных задачах, как правило, значения ограничений ai, bi выбираются из физических или математических соображений.

Например, решение любого уравнения - частный случай этой модели:

f(x)=0

(хотя для решения уравнений есть отдельный инструмент Подбор параметра).

Любая задача об условном экстремуме функции тоже решается тем же методом.

Задачи, изучаемые в математическом программировании, тоже решаются "Поиском решения".

Итак, поиск решения – это процедура нахождения оптимального значения исследуемой функции, отвечающего системе ограничений. В терминологии Excel, целевая ячейка, в которой находится функция, может ссылаться на изменяемые (зависимые) ячейки, в которых содержатся аргументы функции. При этом для каждого аргумента можно задать ограничения. Для запуска поиска решения нужно встать в целевую ячейку и выбрать команду Поиск решения панели Данные (меню Сервис, п. Поиск решения в старых версиях Excel XP/2003).

После этого, выбрав в окне диалога критерий оптимизации (минимальное, максимальное или фиксированное значение целевой функции), нужно сослаться на зависимые ячейки и ввести ограничения в соответствующих полях окна диалога. Ограничения указываются в виде

Зависимая_ячейка Знак Выражение

где Знак может принимать значения <=, =, >= или ограничение до целого числа, если задача целочисленна.

При этом начальные значения зависимых ячеек должны быть таковы, чтобы численный метод оптимизации сходился. Попросту говоря, берите все начальные значения допустимыми ну или нулями, если лень анализировать эту самую "допустимость".

Примечание. Если указанный пункт меню отсутствует, включите соответствующую надстройку в Excel: меню Файл, команда Параметры Excel, вкладка Надстройки, в списке Управление выбрать пункт "Надстройки Excel" и нажать кнопку "Перейти", затем включить надстройку (или меню Сервис, Надстройки в старых версиях Excel).

Пример 1. Фабрика может выпускать продукцию 2 типов - по P1 и P2 рублей за единицу. Для выпуска продукции выделено L единиц ресурсов и T человеко-часов. Известно, что на выпуск единицы продукции 1-го и 2-го вида уходит по ZL1 и ZL2 единиц ресурсов и ZT1 и ZT2 человеко-часов соответственно. Сколько нужно произвести продукции первого и второго видов, чтобы ее общая стоимость была максимальна? Данные взять из приведенной ниже таблицы.

Составим математическую модель задачи и определим целевую функцию. Искомые величины – количество производимой продукции 1 и 2 видов – обозначим как K1 и K2. Тогда целевая функция общей стоимости произведённой продукции записывается как K1*P1+K2*P2 → max. Учтем ограничения на имеющиеся единицы ресурсов и человеко-часы (запасы) неравенствами вида: K1*ZT1 + K2*ZT2 ≤ T ; K1*ZL1 + K2*ZL2 ≤ L. Те факты, что произвести можно только целое и неотрицательное число единиц продукции каждого вида, учтем неравенствами K1≥0; K2≥0; K1=целое, K2=целое.

Введем модель задачи как показано на рисунке:

Выбрав курсором ячейку E4, обратимся к инструменту Поиск решения и введем данные для решения как показано на рисунке:

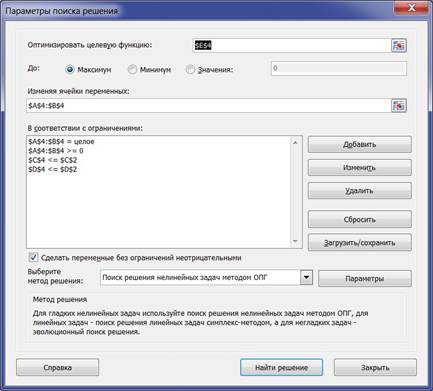
После нажатия кнопки "Выполнить" получим решение K1=15, K2=45

Возможно, в окне поиска решения потребуется дополнительно нажать кнопку "Параметры" и снять флажок "Игнорировать целочисленные ограничения"

Решение задачи в Excel младших версий показано на следующем рисунке.

Пример 2. Есть вот тут про коробку. А вот здесь - про МНК как задачу оптимизации.

Ещё примеры. Нужны были на днях задачи, быстро придумал про цилиндры, а чем плохой объект?

1. Какими должны быть радиус основания r и высота h цилиндра объёмом V=1 м³, чтобы диаметр основания цилиндра как можно меньше отличался от его высоты?

2. Изготовляется полый цилиндр с радиусом основания r см и высотой h см, одно из оснований отсутствует. Минимизируйте общую площадь поверхности цилиндра для объёма 1.2 м³. Допустимые значения величин r и h - от 0.3 до 1 м

3. Прямоугольная заготовка шириной h см сгибается по окружности так, чтобы получился полый цилиндр высотой h см

Шов цилиндра заваривается

К дну также приваривается круглая заготовка радиуса r см

Какими должны быть значения r и h, чтобы минимизировать длину сварного шва для требуемого объёма цилиндра 1 м³?

4. Найдите радиус основания r и высоту h цилиндра максимального объёма, площадь полной поверхности которого составляет 10 м². Толщиной стенок цилиндра можно пренебречь

Надеюсь, анализ решения задач, показанного в прикреплённом ниже архиве, поможет Вам в освоении этого необычайно удобного инструмента.

 4 задачи про цилиндр (Поиск решения) - скачать пример в Excel XP/2003 (39 Кб)

Пример 5. Найти такой равносторонний треугольник, для которого выполняется соотношение P/S=S/P, где S - площадь, P - периметр. Треугольник задан сторонами A, B, C

Модель решения и его графическая иллюстрация показаны на скриншоте, а файл с примером прикреплён под рисунком.

 Задача про треугольник (Поиск решения) - скачать пример в Excel XP/2003 (39 Кб)

гостевая; E-mail