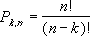
|
Pers.narod.ru. Обучение. Excel: Считаем число перестановок и комбинаций |
Перестановка Ч это любое множество или подмножество объектов или событий, в котором внутренний порядок имеет значение.
Как правило, перестановки считаются для заданного числа объектов, которые выбираются из общего числа объектов.
Традиционно, общее число объектов или событий обозначают N, выбираемое число объектов или событий - K, а число перестановок из N по K обозначают
Pk,n. Существует формула, позволяющая легко определить число перестановок из N по K:
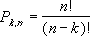
Здесь N! - факториал числа N, то есть, произведение вида 1*2*...*N.
В Excel считать перестановки очень удобно, не нужно даже вычислять факториалы:
=ПЕРЕСТ(N;K)
Вместо N и K задаются целые положительные числа, N≥K.
Например, красный, синий и зелёный шарики можно переставить шестью способами:
=ПЕРЕСТ(3;3)
КСЗ КЗС ЗКС СКЗ СЗК ЗСК
Выбрать 2 рюмки из трёх, стоящих на столе, можно также шестью способами:
=ПЕРЕСТ(3;2)
(1,2), (2,1), (1,3), (3,1), (2,3), (3,2)
Примечание. В русскоязычной литературе такие перестановки,
составленные из n различных элементов выбором по m элементов, которые отличаются либо составом
элементов, либо их порядком,
часто называют размещениями, а под перестановками понимают
всю совокупность комбинаций, состоящих из одних и тех же n различных элементов и отличающихся только порядком их расположения.
В этом смысле число всех возможных перестановок
для множества из n различных элементов считается по формуле
Pn = n!
или в Excel
=ФАКТР(N)
Наши три рюмки можно переставить 6 способами, потому что 3!=3*2*1=6
(1,2,3) (1,3,2) (2,1,3) (2,3,1) (3,1,2) (3,2,1)
Получается, что перестановки выбором всех элементов можно считать частным случаем размещения при n=k.
Кроме перестановок, в комбинаторике различают собственно комбинации или сочетания, в этой задаче считается число всех возможных сочетаний N объектов в группы по K элементов, причём порядок элементов в группе несущественен. В тех же обозначениях, формула для определения числа сочетаний по K объектов из N имеет вид
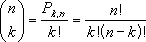
Очень часто число сочетаний из N по K обозначают как CNK.
В Excel число комбинаций считает функция
=ЧИСЛКОМБ(N;K)
Значения N и K также должны быть целыми и положительными, N≥K
С этой точки зрения выбрать 2 рюмки из трёх можно всего тремя способами:
=ЧИСЛКОМБ(3;2)
(1,2), (1,3), (2,3)
![]() В этой статье - реализации основных комбинаторных алгоритмов на Паскале
В этой статье - реализации основных комбинаторных алгоритмов на Паскале
|
Часть 2. Выборки с повторениями в Excel |
Всё, что написано выше, относится к выборкам без повторений, то есть, таким, где все выбираемые элементы различны. Но на практике нам часто попадаются и выборки с повторениями, часть элементов которых неразличима. Например, шары одного цвета, одинаковые буквы или цифры и т.п. Можно понимать повторения и по-другому - предположив, что каждый элемент может участвовать в размещении несколько раз, то есть, элемент возвращается в выборку, повторяется в ней.
Для выборок с повторениями основные комбинаторные формулы будут другими.
Пусть имеется выборка из n элементов, причем k элементов из них - одинаковые.
1. Число различных перестановок элементов такой выборки равно:
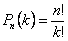
- число перестановок с k повторениями на множестве из n элементов.
Запись в Excel:
=ФАКТР(N)/ФАКТР(K)
Пример: на столе стоит 3 белых рюмки и 1 синяя. Сколько можно сделать различных выборок по 3 рюмки?
Итак, имеем 4 рюмки, 3 из которых - одинаковые. Нам важен также порядок, в котором стоят рюмки. Получаем
4!/3!=4
(Б,Б,С) (Б,С,Б) (С,Б,Б) (Б,Б,Б)
Как быть, если "сортов"объектов больше двух? Ответ - в п. 4
Кстати, если порядок рюмок неразличим, у нас всего 2 варианта:
(Б,Б,Б) (Б,Б,С)
Подумайте - какие здесь работают комбинаторные законы? (см. замечание)
2. Сочетание с повторениями из n элементов по k - неупорядоченная выборка k элементов с возвращением
из множества, содержащего n элементов:
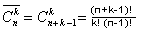
- число различных сочетаний с повторениями из n элементов по k
Запись в Excel (общий вид):
=ЧИСЛКОМБ(N+K-1;K)
Пример. В задаче про 4 рюмки мы теперь как бы возвращаем каждую вынутую рюмку на место, а значит, существует 20 способов выпить трижды с использованием этих четырёх рюмок:
1 1 1 1 1 2 1 1 3 1 1 4 2 2 1 2 2 2 2 2 3 2 2 4 3 3 1 3 3 2 3 3 3 3 3 4 4 4 1 4 4 2 4 4 3 4 4 4 1 2 3 1 2 4 2 3 4 1 3 4
3. Размещения с повторениями из n элементов по k - расположение n различных объектов по k различным ячейкам (местоположениям).
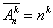
- число различных размещений с повторениями.
Пример - сколько различных 5-буквенных слов можно составить из букв "а" и "б"? У нас 2 объекта-буквы и 5 позиций, куда их можно размещать.
=2^5
Ответ = 32
4. Наконец, верно обобщение первой формулы: число различных перестановок на множестве из n элементов, среди которых имеется
k1 элементов первого вида,
k2 элементов второго вида,
Е
kn элементов n-го вида
равно:
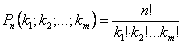
Общий вид формулы в Excel:
=ФАКТР(N)/(ФАКТР(K1)*ФАКТР(K2)*...*ФАКТР(KN))
Пример - сколько различных 5-буквенных слов можно составить из 3 букв "а" и 2 букв "б"?
Обратите внимание на отличие - теперь число объектов (букв) каждого вида фиксировано!
=ФАКТР(5)/(ФАКТР(3)*ФАКТР(2))
Ответ = 10
ааабб аабаб абааб баааб бааба бабаа ббааа аабба абаба аббаа
![]() Файл-пример с реализацией основных комбинаторных формул в Excel (21 Кб)
Файл-пример с реализацией основных комбинаторных формул в Excel (21 Кб)
|
Замечание: об одной комбинаторной задаче |
Хотя выше я и писал:
Кстати, если порядок рюмок неразличим, у нас всего 2 варианта:(Б,Б,Б) (Б,Б,С)Подумайте - какие здесь работают комбинаторные законы?
На самом деле, думать можно очень долго - под известные комбинаторные формулы такая задача просто не подходит. В общем виде условие можно сформулировать так:
Имеется N объектов, относящихся к L сортам.
Количество объектов каждого сорта известно и равно k1, k2, ..., kL,
сумма ki=N.
Определить число различных сочетаний по M объектов из N, если объекты,
относящиеся к одному сорту, считаются неразличимыми между собой.
Доступный пример: N=4, L=2, k1=3, k2=1, M=3, например, имеем 3 белых рюмки и 1 синюю.
Число сочетаний по 3 из 4 равно в данном случае 2 - (Б, Б, Б) и (Б, Б, C).
Формула числа сочетаний С43 даст 4, так как в ней все объекты считаются различимыми.
Под сочетания с повторениями, число которых здесь = 20, наш случай тем более не подходит - неразличимы-то только объекты одного вида.
Известная формула
для числа различных перестановок на множестве из n элементов, среди которых имеется
ki элементов i-го вида -
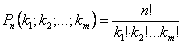 нам тоже не подойдёт, у нас не перестановки.
нам тоже не подойдёт, у нас не перестановки.
Видимо, решать нужно так:
найти число решений уравненияx1 + ... + xL = M
при ограничениях
0 <= x1 <= k1, ..., 0 <= xL <= kL
Формула для числа решений выводится при этом индуктивно.
Фактически, всё свелось к решению диофантова уравнения "в общем виде", а это невозможно (десятая проблема Гильберта, алгоритмическая неразрешимость которой считается доказанной). Похоже, что простой замкнутой формулы нет в принципе. Сложный расчёт с вложенными суммами можно сделать, но вычисление по такой формуле-монстру мало чем будет отличаться просто от перебора. Ещё существуют производящие функции - но практический счёт они никак не упростят. Лучше всего - рекуррентный подсчёт с конкретными числами.
Ну а само по себе приведённое уравнение вполне исследовано -
например, известно, что
диофантово уравнение x1 + ... + xL = M имеет
СM-1L-1 различных решений в натуральных числах.
Увы, нам это не поможет - скажем, имеем 3 белых рюмки, 2 синих, выбираем всего 2
(L=2, M=2, формула даёт C11, на самом деле ответ = 3 (ББ, БС, СС).
Если учесть "вырожденные" решения уравнения, то есть, случаи, когда
какого-то вида объектов нет в наборе, и соответствующий xi=0, для него формула будет
CM+L-1L-1
Пример того, что и эта формула не подходит - 3 белых, 1 синяя, выбираем всего 3 (L=2, M=3): C41=4
Это потому, что посчитались и те комбинации, для которых не хватит рюмок (2 последних):
ББС БББ БCC ССС
Можно попытаться вычитать из СM+L-1L-1 (число сочетаний с перестановками для нашей задачи)
все лишние "цэшки", которые получаются при ki<M (если не хватает рюмок какого-то вида, их число меньше числа выбираемых M),
я попытался... Убив кучу времени, получил дикую и неуниверсальную при этом формулу,
убедился в правильности выделенного красным :)
Вот здесь есть скрипт-решалка для одного класса линейных диофантовых уравнений.
|
|