Решение обыкновенных дифференциальных уравнений (ОДУ) - популярный раздел численных методов, немного теории можно почитать здесь.

В приведённом примере решается задача Коши, то есть, ищется решение дифференциального уравнения первого порядка вида dy/dx = f(x,y) на интервале x ∈ [x0,xn] при условии y(x0)=y0 и равномерном шаге сетки по x.

Решение выполняется методами Эйлера, "предиктор-корректор" (он же модифицированный метод Эйлера) и методом Рунге-Кутта 4 порядка точности. Пример может служить образцом для Ваших решений, правда, функцию придётся перепрограммировать несколько раз при различных значениях аргумента - поскольку без применения макросов на VBA Excel не позволяет создать полноценную функцию, которую было бы удобно вызывать с разными значениями аргументов.

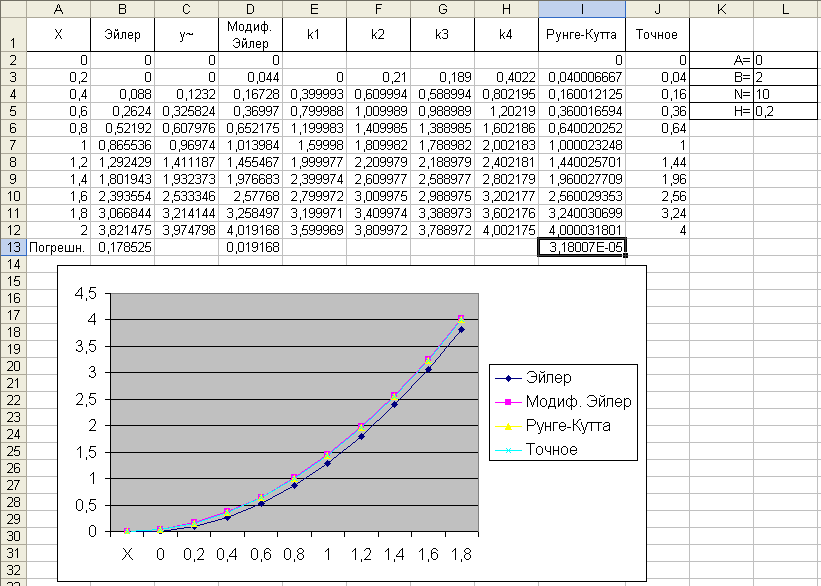
Здесь решается уравнение dy/dx = 2x-y+x2 на интервале [0,2], начальное значение y(0)=0, для оценки точности задано также точное решение в виде функции u(x)=x2. Оценка погрешности делается в норме L1, как и принято в данном случае.

 Скачать пример в Excel XP/2003 (28 Кб)

гостевая; E-mail