|
Pers.narod.ru. Обучение. Интерполяционный полином Ньютона |
Дана таблица значений функции y = f(x)
|
x |
x0 |
x1 |
... |
xn |
|
y |
y0 |
y1 |
... |
yn |
и два значения аргумента x= a и x = b, отличные от данных в таблице. Требуется с помощью полиномов Ньютона третьей степени вычислить приближенные значения функции y = f(x) в точках x = a и x = b, т.е. f(a) и f(b).
Пример решения
|
x |
1.6 |
1.7 |
1.8 |
1.9 |
2.0 |
a = 1.92 |
|
y |
1.6416 |
2.3961 |
3.3536 |
4.5441 |
6.0000 |
b = 1.68 |
Построим таблицу конечных разностей:
|
i |
xi |
yi |
Δyi |
Δ2yi |
Δ3yi |
|
0 |
1.6 |
1.6416 |
0.7545 |
0.2030 |
0.0300 |
|
1 |
1.7 |
2.3961 |
0.9575 |
0.2330 |
0.0324 |
|
2 |
1.8 |
3.3536 |
1.1905 |
0.2654 |
|
|
3 |
1.9 |
4.5441 |
1.4559 |
|
|
|
4 |
2.0 |
6.0000 |
|
|
|
Поскольку точка b = 1.68 находится ближе к началу таблицы, а точка a = 1.92 – ближе к концу таблицы, то для нахождения значения f(b) будем использовать первый полином Ньютона, а для нахождения f(a) – второй. Ближайшее меньшее к точке b значение узла таблицы = 1.6, а ближайшее большее к точке a = 2.
Выпишем первый и второй полиномы третьей степени:
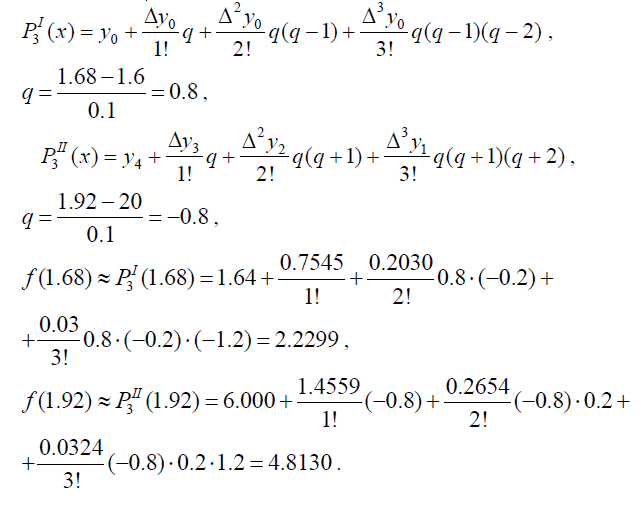
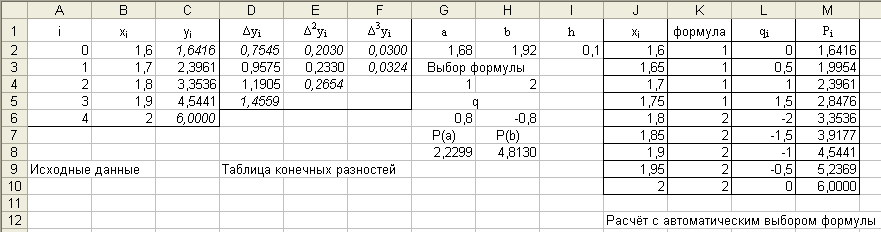
Скриншот реализации задачи в Excel показан ниже. Значения полинома вычисляются в точках a и b,
а также строятся значения полинома в пределах изменения x с шагом, равным 0.05 и автоматическим выбором первой или второй формулы.
Интерполяционный полином Ньютона - скачать пример в Excel XP/2003 (28 Кб)
Следует учесть, что в документе расчёт делается всегда по первым конечным разностям (от точек y0, y1), если точка a или b лежит ближе к началу интервала, и по последним (от точек y3, y4), если она ближе к концу. Есть и другие способы расчёта, берущие ближайший слева или справа узел.
 гостевая; E-mail
|
