Pers.narod.ru. Алгоритмы. Простые алгоритмы сортировки одномерного массива

Этот сайт больше не обновляется. Подключите Javascript, чтобы увидеть новый адрес страницы или перейдите к статье

Сортировка выбором

Начинаем с первого элемента массива. Ищем в массиве наименьший элемент m и меняем его местами с первым. Поскольку наименьший элемент массива после перестановки гарантированно размещается на первом месте, дальнейший поиск начинаем со второго элемента и меняем местами второй с наименьшим из оставшихся. Таким образом, получаем двойной цикл сортировки.

Здесь показана сортировка по возрастанию, сортировка по убыванию будет отличаться только тем, что во внутреннем цикле ищется не минимальный, а максимальный элемент массива.

Кроме того, первый листинг покажем полностью, а потом будем только менять процедуру сортировки Sort1 на Sort2 и т.п.

uses crt;
 
procedure GenerateArray (n:integer; var a:array of integer);
{заполняет n элементов целочисленного массива a случайными числами от 1 до 100}
var i:integer;
begin
 randomize;
 for i:=Low(a) to Low(a)+n-1 do a[i]:=1+random(100);
end;
 
procedure PrintArray (n:integer; var a:array of integer);
{вывод n элементов целочисленного массива a в строку с новой строки экрана}
var i:integer;
begin
 writeln;
 for i:=Low(a) to Low(a)+n-1 do write (a[i],' ');
end;
 
procedure Wait; {Ожидание нажатия Enter}
begin
 writeln;
 write ('Нажмите Enter для продолжения...');
 reset (input); readln;
end;
 
procedure Sort1 (n:integer; var a:array of integer);
{Сортировка выбором}
var m,k,i,j,n1,n2:integer;
begin
 n1:=Low(a); n2:=Low(a)+n-1; {если делать без открытых массивов,
  можно заменить на 1 и n соответственно!}
 for i:=n1 to n2-1 do begin
  m:=a[i];
  k:=i; {иначе будут проблемы при уже упорядоченных элементах}
  for j:=i+1 to n2 do
   if a[j]<m then begin
    m:=a[j]; k:=j;
   end;
  if k<>i then begin a[k]:=a[i]; a[i]:=m; end;
 end;
end;
 
var a:array [1..100] of integer;
 
begin
 clrscr;
 GeneRateArray (10,a);
 write ('Исходный массив');
 PrintArray (10,a);
 writeln; write ('Отсортированный массив');
 Sort1 (10,a);
 PrintArray (10,a);
 Wait;
end.

"Трудоёмкость" этого алгоритма (число выполняемых сравнений элементов) можно оценить по формуле (n²-n)/2 для массива из n элементов.

Сортировка обменами (метод пузырька)

В этом методе организуется последовательный перебор элементов массива A₁, A₂, ... A_N и сравнение значений 2 соседних элементов. Если впереди находится элемент с большим значением, выполняется перестановка (при сортировке по возрастанию). Сортировка по убыванию будет отличаться только знаком операции (<, а не >) в операторе сравнения соседних элементов. Переменная m теперь используется как буфер для перестановки 2 соседних элементов в массиве.

Этот метод называют также методом пузырька, так как при его реализации наибольшие или наименьшие текущие элементы как пузырьки "поднимаются" к началу массива (или "опускаются" к его концу).

procedure Sort2 (n:integer; var a:array of integer);
{Сортировка обменами (метод пузырька)}
var m,i,j,n1,n2:integer;
begin
 n1:=Low(a); n2:=Low(a)+n-1;
 for i:=n1 to n2-1 do
 for j:=n1 to n2-i-1 do
  if a[j]>a[j+1] then begin
   m:=a[j]; a[j]:=a[j+1]; a[j+1]:=m;
  end;
end;

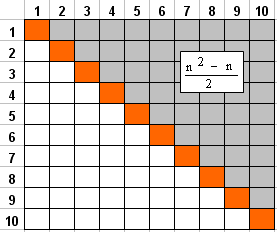
Число сравнений оценивается аналогично. Вообще, при сравнении элементов массива по принципу "каждый с каждым" проще всего представить эти элементы в виде прямоугольной таблицы-матрицы. Поскольку сравнить элементы 1 и 3 - то же самое, что сравнить 3 и 1, а сравнивать элемент с самим собой не нужно, получаем, что из n² всех возможных сравнений нужно отнять n элементов на главной диагонали ("сравнения элемента с самим собой") и взять от этой величины половину:

Сортировка простыми вставками

Последовательно просматриваем элементы массива A₁, A₂, ... A_N и каждый просматриваемый элемент этой последовательности вставляем на подходящее место в уже упорядоченную последовательность A₁, ... A_i. Место вставки определяется последовательным сравнением значения A₁ с предварительно упорядоченными значениями A₁, ... A_i-1. Затем в найденном месте соседние элементы массива "раздвигаются", освобождая место под вставляемый элемент.

Для сортировки по убыванию по-прежнему достаточно заменить знак в операции сравнения - ">" на "<". Переменная m в третьей функции также служит для задачи обмена значений элементов массива.

procedure Sort3 (n:integer; var a:array of integer);
{Сортировка простыми вставками}
label m1;
var m,i,j,k,n1,n2:integer;
begin
 n1:=Low(a); n2:=Low(a)+n-1;
 for i:=n1+1 to n2 do begin
  for j:=i-1 downto n1 do
   if a[i]>a[j] then goto m1;
  j:=n1-1;
 m1:
  m:=a[i];
  for k:=i downto j+2 do a[k]:=a[k-1];
  a[j+1]:=m;
 end;
end;

При "удачных" данных алгоритм выполнит меньше сравнений за счёт оператора break; - досрочного выхода из вложенного цикла, но надо учесть, что есть ещё цикл по k. В реальной программе, особенно системного уровня, этот цикл стоило бы заменить быстрым "сдвигом" адресов элементов массива в памяти.

Существуют и значительно более мощные алгоритмы сортировки, однако, их применение имеет смысл для действительно больших объемов данных.

Я обычно пользуюсь сортировкой, описанной в этой главе учебника - что-то "среднее" между выбором и обменами с тем же числом сравнений.

Пара примеров по сортировке одномерного массива, выполненной на консольном Си:

/*
 Программа сортировки элементов одномерного целочисленного массива размерностью 10
*/
#include <iostream.h>
#include <stdlib.h>
void main() {
 int a[10],i,j,c;
 randomize();
 cout << endl <<"massiv do sortirovki ";
 for (i=0;i<10;i++){
  a[i]=random (10);
  cout <<a[i] << " ";
 }
 
 for (i=0;i<9;i++)
 for (j=i+1;j<10;j++)
 if (a[i]>a[j]) {
  c=a[i];
  a[i]=a[j];
  a[j]=c;
}
 
 cout << endl <<"massiv posle ";
 for (i=0;i<10;i++) cout<<a[i] << " ";
}
 
  
/*
 Программа сортировки элементов одномерного целочисленного массива размерностью 10
 Метод пузырька (сортировка обменами)
 Число сравнений неоптимально, как его уменьшить?
*/
 
#include <iostream.h>
#include <conio.h>
#include <dos.h>
#include <stdlib.h>
 
void main() {
int a[10],i,j,c;
randomize();
for (i=0;i<10;i++) a[i]=random (10);
 
for (j=0;j<9;j++)
for (i=0;i<9;i++)
 if (a[i]>a[i+1]) {
  c=a[i];
  a[i]=a[i+1];
  a[i+1]=c;
  clrscr ();
  for (int k=0; k<10; k++) cprintf ("%d  ",a[k]);
  delay (500);
 }
 
cout << endl <<"massiv posle ";
for (i=0;i<10;i++) cout<<a[i] << " ";
 
}

гостевая; E-mail