Треугольник на плоскости задан координатами вершин A, B, C. Определить, попадает ли точка D в треугольник.

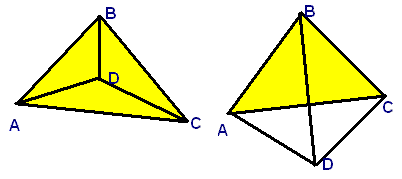
Первое, что приходит в голову - посчитать сумму площадей треугольников ABD, ACD и BCD, образованных соединением точки D с вершинами треугольника:

Точка находится в треугольнике тогда и только тогда, когда сумма площадей этих 3 треугольников равна площади исходного треугольника ABC. Сами площади, при известных координатах всех точек, легко высчитать по формуле Герона (функция S). Вот реализация на Паскале, каждая точка на плоскости описана с помощью пользовательского типа данных Point.

type point= array [1..2] of real;

function dist (a,b:point):real;
begin
 dist:=sqrt(sqr(a[1]-b[1])+sqr(a[2]-b[2]));
end;

function s (a,b,c:point):real;
var l1,l2,l3,p:real;
begin
 l1:=dist(a,b);
 l2:=dist(a,c);
 l3:=dist(b,c);
 p:=(l1+l2+l3)/2;
 s:=sqrt(p*(p-l1)*(p-l2)*(p-l3));
end;

const a:point=(0,0);
      b:point=(4,0);
      c:point=(4,5);
var d:point;
    p1,p2:real;
begin
 d[1]:=1;
 d[2]:=1.2;
 p1:=s(a,b,d)+s(a,c,d)+s(b,c,d);
 p2:=s(a,b,c);
 writeln (p1:8:2,p2:8:2, (abs(p1-p2)<1e-8):6);
end.

Недостатки подхода очевидны - во-первых, нужно сравнивать вещественные числа, что, вообще говоря, некорректно (в программе числа сравниваются с произвольно выбранной точностью 10^-8) во-вторых, нужна операция извлечения квадратного корня, что потенциально снижает точность расчётов (попробуйте, например, для треугольника с координатами вершин (0,0), (0,10000000), (1,10000000)). В третьих, кстати, неясно, как быть, когда точка лежит на одной из сторон треугольника.

Подход можно изменить - скажем, считать расстояния от точки D до точек A, B, C и периметр исходного треугольника. Если сумма трёх расстояний меньше периметра, то точка находится внутри треугольника. Однако, недостатки метода при таком подходе сохраняются.

Это не работает, скажем, для тупоугольных треугольников. Контрпример - треугольник с вершинами (-2,2), (3,1), (0,1) и точка (0,0)

Наконец, можно попробовать обойтись только разностями между проекциями точек на оси координат и операцией умножения. Думаю, этот вариант близок к оптимальному, вот изменённая версия программы:

type point= array [1..2] of real;

function PointInTriangle (a,b,c,p:point):boolean;
begin
 PointInTriangle:=false;
 if ((p[1]-a[1])*(a[2]-b[2])-(p[2]-a[2])*(a[1]-b[1])>=0) and
    ((p[1]-b[1])*(b[2]-c[2])-(p[2]-b[2])*(b[1]-c[1])>=0) and
    ((p[1]-c[1])*(c[2]-a[2])-(p[2]-c[2])*(c[1]-a[1])>=0) then PointInTriangle:=true;
end;

const a:point=(0,0);
      b:point=(4,0);
      c:point=(4,5);
var d:point;
    p1,p2:real;
begin
 d[1]:=1;
 d[2]:=1.2;
 writeln (PointInTriangle(a,b,c,d):6);
end.

Для корректной работы этого кода вершины должны быть перечислены в порядке против часовой стрелки, так что при необходимости нужно их сначала сортировать.

гостевая; E-mail