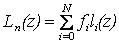Pers.narod.ru. Алгоритмы. Реализация основных методов интерполяции функции одной переменной

1. Постановка задачи

Задана исходная функция ln((x2-3x+2)/(x2+1)) и интервал [0,1]. Построить узлы интерполяции xi =a+h*i, i=0,1,...,N, h=(b-a)/N, (N - параметр задачи), и вычислить в этих узлах значения fi= g(xi). Вычисленные значения xi, fi занести в массивы.

Написать программу для нахождения значения F(z) в некоторой произвольной точке z принадлежит [a,b], не совпадающей ни с одним из узлов xi с помощью кусочно-постоянной интерполяции. Значение z вводить с клавиатуры. Найти погрешность метода |g(z)-F(z)|, вывести на печать. Составить таблицу поведения погрешности в зависимости от N=10, 20, 40, 80.

Написать программу для нахождения значения F(z) в некоторой произвольной точке z принадлежит [a,b] с помощью кусочно-линейной интерполяции. Значение z вводить с клавиатуры. Найти погрешность метода |g(z)-F(z)|, вывести на печать. Составить таблицу поведения погрешности в зависимости от N=10, 20, 40, 80.

Написать программу для вычисления значения полинома Лагранжа LN(z), где z - произвольная точка из отрезка [a,b], не совпадающая ни с одним из узлов xi. Попробовать различные точки z: близко к левому концу отрезка [a,b], в средней части, близко к правому концу. Найти погрешность метода |g(z)-F(z)|, вывести на печать. Составить таблицу поведения погрешности в зависимости от N=10, 20, 40, 80.

2. Описание методов интерполяции

Кусочно-постоянная интерполяция. Пусть z принадлежит [xi-1, xi], i=1,2,..,N. Искомая функция является постоянной и равна левому: Fi(z)=fi или правому: Fi(z)=fi значению. Условия интерполяция выполняются, однако найденная функция является разрывной.

Кусочно-линейная интерполяция. На каждом интервале функция является линейной Fi(z)=kiz+ci; значения коэффициентов находятся из выполнения условий интерполяции и непрерывности интерполирующей функции: Fi(xi-1)= fi-1, Fi(xi)= fi. Итоговая функция будет непрерывной, но производная будет разрывной в каждом узле интерполяции.

Полином Лагранжа ,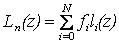

где 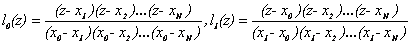и т.д.

В общем случае 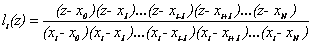, i=0,1,2,...,N.

3. Тексты программ

Формирование таблиц исходных данных (файл 10.dat, 20.dat, 40.dat, 80.dat для N=10,20,40,80 соответственно).

program Tabl; {01.pas}
const n:array [1..4] of integer=(10,20,40,80);
var
h,a,b,x,y:real;
i,r:integer;
f1:text;
name:string;
 
function f(x:real):real;
begin
 f:=ln( (sqr(x)-3*x+2)/(sqr(x)+1) );
end;
 
begin
 writeln ('a,b? ');
 readln (a,b);
 for r:=1 to 4 do begin
  h:=(b-a)/n[r];
  str(n[r]:2,name);
  name:=Concat (name,'.dat');
  assign (f1,name);
  rewrite (f1);
  for i:=0 to n[r] do begin
   x:=a+i*h;
   y:=f(x);
   writeln(f1,x,' ',y);
  end;
  writeln ('file ',name,' OK for N=',n[r]);
  close (f1);
 end;
end.

Кусочно-постоянная интерполяция

program Post; {02.pas}
const n:array [1..4] of integer=(10,20,40,80);
var a,b,z,fx:real;
    x,y:array[0..100] of real;
    i,r,n1,num:integer;
    f1:text;
name:string;
 
function f(x:real):real;
begin
 f:=ln( (sqr(x)-3*x+2)/(sqr(x)+1) );
end;
 
begin
 writeln ('Z? ');
 readln (z);
 writeln ('n':5,'g(z)':15,'f(z)':15,'|g(z)-f(z)|':15);
 for r:=1 to 4 do begin
  str(n[r]:2,name);
  name:=Concat (name,'.dat');
  assign (f1,name);
  reset (f1);
  i:=0;
  while not eof(f1) do begin
   readln (f1,x[i],y[i]);
   i:=i+1;
  end;
  close (f1);
  n1:=i-1;
  a:=x[0];
  b:=x[n1];
  if z<a then fx:=y[0]
  else if z>b then fx:=y[n1]
  else begin
   num:=Trunc((z-a)*n1/(b-a));
   fx:=y[num];
  end;
  writeln (n1:5,fx:15:10,f(z):15:10,abs(fx-f(z)):15:10);
 end;
end.

Кусочно-линейная интерполяция

program Linear; {03.pas}
const n:array [1..4] of integer=(10,20,40,80);
var a,b,z,fx,a1,b1:real;
    x,y:array[0..100] of real;
    i,r,n1,num:integer;
    f1:text;
name:string;
 
function f(x:real):real;
begin
 f:=ln( (sqr(x)-3*x+2)/(sqr(x)+1) );
end;
 
begin
 writeln ('Z? ');
 readln (z);
 writeln ('n':5,'g(z)':15,'f(z)':15,'|g(z)-f(z)|':15);
 for r:=1 to 4 do begin
  str(n[r]:2,name);
  name:=Concat (name,'.dat');
  assign (f1,name);
  reset (f1);
  i:=0;
  while not eof(f1) do begin
   readln (f1,x[i],y[i]);
   i:=i+1;
  end;
  close (f1);
  n1:=i-1;
  a:=x[0];
  b:=x[n1];
  if z<=a then fx:=y[0]
  else if z>=b then fx:=y[n1]
  else begin
   num:=Trunc((z-a)*n1/(b-a));
   {коэффициенты прямой от точки (x[i],y[i]) до (x[i+1],y[i+1])}
   a1:=(y[num]-y[num+1])/(x[num]-x[num+1]);
   b1:=y[num]-a1*x[num];
   fx:=a1*x[num]+b1;
  end;
  writeln (n1:5,fx:15:10,f(z):15:10,abs(fx-f(z)):15:10);
 end;
end.

Полином Лагранжа

program Lagr; {04.pas}
type vector=array[0..100] of real;
const n:array [1..4] of integer=(10,20,40,80);
var a,b,z,fx,a1,b1:real;
    x,y:vector;
    i,r,n1,num:integer;
    f1:text;
name:string;
 
function f(x:real):real;
begin
 f:=ln( (sqr(x)-3*x+2)/(sqr(x)+1) );
end;
 
function Lagrange (n:integer; var x,f:vector; x0:real):real;
var i,j:integer;
    p,s:real;
begin
 s:=0;
 for i:=0 to n do begin
  p:=1;
  for j:=0 to n do begin
   if i<>j then p:=p*((x0-x[j])/(x[i]-x[j]));
  end;
  s:=s+f[i]*p;
 end;
 Lagrange:=s;
end;
 
begin
 writeln ('Z? ');
 readln (z);
 writeln ('n':5,'g(z)':15,'f(z)':15,'|g(z)-f(z)|':15);
 for r:=1 to 4 do begin
  str(n[r]:2,name);
  name:=Concat (name,'.dat');
  assign (f1,name);
  reset (f1);
  i:=0;
  while not eof(f1) do begin
   readln (f1,x[i],y[i]);
   i:=i+1;
  end;
  close (f1);
  n1:=i-1;
  a:=x[0];
  b:=x[n1];
  if z<=a then fx:=y[0]
  else if z>=b then fx:=y[n1]
  else begin
   fx:=Lagrange (n1,x,y,z);
  end;
  writeln (n1:5,fx:15:10,f(z):15:10,abs(fx-f(z)):15:10);
 end;
end.
4. Результаты расчетов

Формирование файлов данных

a,b?
0 0.99
file 10.dat OK for N=10
file 20.dat OK for N=20
file 40.dat OK for N=40
file 80.dat OK for N=80

Не вводим интервал [0,1], т.к. именно у этой функции в x=1 особенность :)

График интерполируемой функции

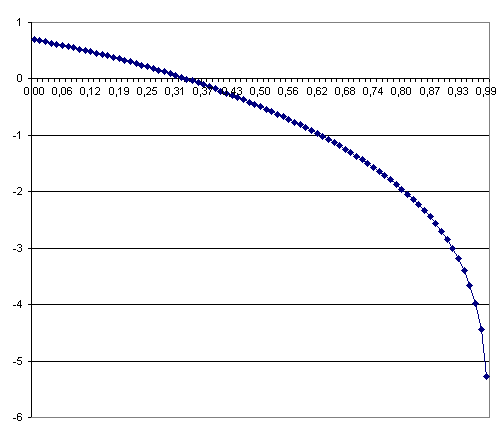
Кусочно-постоянная интерполяция

Z?
0.47
    n           g(z)           f(z)    |g(z)-f(z)|
   10  -0.1773519752  -0.4091988287   0.2318468535
   20  -0.3295804736  -0.4091988287   0.0796183552
   40  -0.3295804736  -0.4091988287   0.0796183552
   80  -0.3694280026  -0.4091988287   0.0397708262

Кусочно-линейная интерполяция

Z?
0.47
    n           g(z)           f(z)    |g(z)-f(z)|
   10  -0.1773519752  -0.4091988287   0.2318468535
   20  -0.3295804736  -0.4091988287   0.0796183552
   40  -0.3295804736  -0.4091988287   0.0796183552
   80  -0.3694280026  -0.4091988287   0.0397708262

Полином Лагранжа

Точка в левой части отрезка

Z?
0.07
    n           g(z)           f(z)    |g(z)-f(z)|
   10   0.5847133934   0.5800612760   0.0046521174
   20   0.5799415750   0.5800612760   0.0001197010
   40   0.5800624092   0.5800612760   0.0000011332
   80 -47.3439597970   0.5800612760  47.9240210730

Точка в середине отрезка

Z?
0.47
    n           g(z)           f(z)    |g(z)-f(z)|
   10  -0.4090353367  -0.4091988287   0.0001634920
   20  -0.4091988939  -0.4091988287   0.0000000651
   40  -0.4091988287  -0.4091988287   0.0000000000
   80  -0.4091988287  -0.4091988287   0.0000000000

Точка в правой части отрезка

Z?
0.92
    n           g(z)           f(z)    |g(z)-f(z)|
   10  -3.1078544062  -3.0620054005   0.0458490056
   20  -3.0607425377  -3.0620054005   0.0012628628
   40  -3.0620056491  -3.0620054005   0.0000002486
   80-109.2519895900  -3.0620054005 106.1899841900
5. Выводы

Как видно из таблиц анализа погрешности, наиболее точным является метод интерполяции с помощью полинома Лагранжа. Однако, погрешность полинома Лагранжа может существенно увеличиться на концах отрезка при слишком большом числе отрезков интерполяции.

 Скачать файлы с программами и данными из этой статьи: pas_interp.zip (5 Кб)

Рейтинг@Mail.ru

вверх гостевая; E-mail
Hosted by uCoz