Метод трапеций.

Суть метода - проведение прямой через значения функции на границах каждого интервала интегрирования. Приближенное значение интеграла на интервале [x_i,x_i+h], где h - шаг по x, определяется по формуле h*(f(x_i)+f(x_i+h))/2+R, где R - априорная погрешность.

Метод Симпсона.

Подынтегральная функция заменяется полиномом 2-й степени - параболой, проходящей через точки x_i,x_i+1,x_i+2. В этом случае на интервале [x_i,x_i+2h] получаем значение интеграла по формуле [f(x_i)+4f(x_i+1)+f(x_i+2)]*h/3

Метод разложения функции в ряд (метод Гаусса с двумя узлами). В этих методах функция приближается полиномами различных степеней, но узлы для построения полиномов выбираются из условия обеспечения минимальной погрешности интегрирования. В методе Гаусса с 2 узлами интеграл на отрезке интегрирования ищется по формуле , где , ,

Поскольку точное значение искомого интеграла равно 0, оценим сравнительную погрешность методов, вычисляя ее по формуле

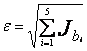, где J_bi - значения интеграла, вычисленные при заданных b_i= {0.5,0.8,1.2,1.5,2.2}

Полученные оценки погрешности

Метод трапеций                   0.066703

Метод Симпсона                  0.066618

Метод Гаусса                        0.00672363

Вывод: наиболее точные результаты дал метод Гаусса, что согласуется с теорией.

#include <conio.h>
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <graphics.h>

float f (float x) { //Функция, интеграл от которой берется
 return x*x*atan(x);
}

float Trap (float x0,float h,float x1) { //Метод трапеций
 float x,s;
 s=(f(x0)+f(x1))/2;
 for (x=x0+h; x<x1; x+=h) {
  s+=f(x);
 }
 return s*h;
}

float Simpson (float x0,float h,float x1) { //Метод Симпсона
 float x,s;
 int i,n;
 n=(x1-x0)/h;
 s=(f(x0)+f(x1))/2+2*f(x0+h/2);
 x=x0;
 for (i=0; i<n-1; i++) {
  x+=h;
  s+=(2*f(x+h/2)+f(x));
 }
 return s*h/3;
}

float Gauss (float x0,float h,float x1) { //Разложение в ряд
 float x,c,d,s;
 int n,i;
 c=h/sqrt(3);
 d=h-c;
 x=x0+d/2;
 s=0;
 n=(x1-x0)/h;
 for (i=0; i<n; i++) {
  s+=f(x);
  x+=c;
  s+=f(x);
  x+=d;
 }
 return s*h/2;
}

void Init (void) { //Открытие графики
 int gdriver = VGA, gmode=VGAHI, errorcode;
 registerbgidriver(EGAVGA_driver);
 initgraph(&gdriver, &gmode, "");
 errorcode = graphresult();
 if (errorcode != grOk) {
  printf("Graphics error: %s\n", grapherrormsg(errorcode));
  printf("Press any key to halt");
  getch();
  exit(1);
 }
}

#define DX 10    /* Отступы по */
#define DY 10    /* X и Y */
#define CEPS 1e-6 /* Точность для циклов с вещ. числами */

void GraphOfFun (float x0, float x1) {
//	График функции f(x)
//	x0,x1 - границы по x
//	Шаг по x выбирается, исходя из разрешения монитора
 int i,j,flag=0,i0,j0;
 float x,fx,fmin,fmax;
 char *str="00000.000";
 //Первый проход - выяснить верхнюю и нижнюю границы по Y
 x=x0;
 fmin=f(x0); fmax=f(x0);
 while (x<=x1+CEPS) {
  if (f(x)>fmax) fmax=f(x);
  else if (f(x)<fmin) fmin=f(x);
  x+=0.001;
 }

 if ((x0<0) && (x1>0)) {
  setcolor (RED);
  i=DX-x0*(getmaxx()-2*DX)/(x1-x0);
  line (i,DY-1,i,getmaxy()-DY+1);
 }
 if ((fmin<0) && (fmax>0)) {
  setcolor (RED);
  j=getmaxy()-(DY-fmin*(getmaxy()-2*DY)/(fmax-fmin));
  line (DX,j,getmaxx()-DX,j);
 }
 //Нарисовать обрамление
 setcolor (YELLOW);
 rectangle (DX-1, DY-1, getmaxx()-DX+1, getmaxy()-DY+1);
 gcvt (x0,3,str); outtextxy (DX,getmaxy()-DY+2,str);
 gcvt (x1,3,str);
 outtextxy (getmaxx()-DX-textwidth(str),getmaxy()-DY+2,str);
 settextstyle (DEFAULT_FONT, VERT_DIR, 1);
 settextjustify (LEFT_TEXT, BOTTOM_TEXT);
 gcvt (fmin,3,str); outtextxy (DX-2, getmaxy()-DY-2, str);
 settextjustify (LEFT_TEXT, TOP_TEXT);
 gcvt (fmax,3,str); outtextxy (DX-2, DY+2, str);
 setcolor (GREEN);
 //Второй проход - нарисовать график
 i=DX;
 while (i<=getmaxx()-DX) {
  //Пересчитать i на экране в координату x на плоскости
  x=x0+(i-DX)*(x1-x0)/(getmaxx()-2*DX);
  //Вычислить f(x)
  fx=f(x);
  //Пересчитать f в экранные координаты
  j=DY+(fx-fmin)*(getmaxy()-2*DY)/(fmax-fmin);
  j=getmaxy()-j; //"Перевернули" график
  putpixel (i,j,GREEN);
  if (flag==0) { flag=1; i0=i; j0=j; }
  if (j!=j0) line (i0,j0,i,j);
	//Соединили с пред. точкой, чтоб не было видимых разрывов
  i0=i; j0=j;
  i++;
 }
}

void main (void) {
 float r,eps;
 float b[5]={0.5,0.8,1.2,1.5,2.2};
 int i,ch;
 do {
  clrscr();
  printf ("\n Нажмите клавишу для выбора действия:");
  printf ("\n 1. Вычисление интеграла методом трапеций");
  printf ("\n 2. Вычисление интеграла методом Симпсона");
  printf ("\n 3. Вычисление интеграла разложением в ряд");
  printf ("\n 0. Выход из программы\n ");
  fflush(stdin);
  ch=getchar();
  switch (ch) {
   case '1':
   case '2':
   case '3':
    eps=0;
    for (i=0; i<5; i++) {
     if (ch=='1')
      r=Trap (-b[i],(2*b[i])/100,b[i]);
     else if (ch=='2')
      r=Simpson (-b[i],(2*b[i])/100,b[i]);
     else if (ch=='3')
      r=Gauss (-b[i],(2*b[i])/100,b[i]);
     eps+=r*r;
     printf ("\n Значение интеграла, вычисленное при b=%g равно %g",b[i],r);
    }
    eps=sqrt(eps);
    printf ("\n Eps=%g",eps);
    printf ("\n Нажмите любую клавишу для вывода графика...");
    fflush (stdin);
    getchar();
    Init();
    GraphOfFun (-b[2],b[2]);
    fflush (stdin);
    getchar();
    closegraph();
   break;
   case '0': clrscr; return;
   default: break;
  };
 } while (1);
}

 Архив ZIP с файлами, запускать .BAT (53 Кб)

Проблемы с DOS-графикой? Информация здесь

гостевая; E-mail