, 
значения
a, b вводятся пользователем.|
Pers.narod.ru. Обучение. Учебник по Паскалю. Глава 11 |
Итак, основное назначение циклов -- обработка большого объема данных. Математически эта обработка зачастую сводится к поиску, выбору и статистической обработке нужных величин. Практически в любой реальной задаче мы ищем максимальные и минимальные значения в наборе данных, суммируем или перемножаем требуемые данные, определяем арифметическое среднее или количество элементов, отвечающих условию. Для решения всех этих распространенных задач существуют типовые алгоритмы, задающие правила выполнения соответствующих расчетов. Изучением этих алгоритмов мы займемся в гл. 11 и 12.
Разумеется, настоящие задачи, встающие перед программистами, значительно сложнее, чем приведенные далее примеры, но из типовых алгоритмов, как из кирпичиков, строится здание любой сложной программы.
Применяется для составления всевозможных таблиц, которыми могут быть как абстрактная таблица значений математической функции, так и конкретная таблица стоимости товара или платежей, совершенных абонентом сотового оператора.
В общем виде алгоритм можно описать так:
1. до цикла задается начальное значение управляющей переменной, условием выхода из цикла служит достижение управляющей переменной конечного значения;
2. в теле цикла на каждом шаге вычисляется очередное значение функции, зависящее от управляющей переменной, затем формируется строка таблицы;
3. в конце шага цикла значение управляющей переменной (обозначим ее x) изменяется оператором вида x:=x+d;, где d -- заданный шаг по управляющей переменной.
В качестве примера составим таблицу синусов в пределах от 0 до π с шагом по аргументу 0.25. Обозначим аргумент как x, значение синуса от x обозначим как y. В простейшем случае программа табулирования может выглядеть так:
var x,y:real;
begin
writeln('x':10,'sin(x)':10);
{печать заголовка таблицы до цикла}
x:=0; {начальное значение аргумента}
while x<=pi+1e-6 do begin
y:=sin(x); {вычисление функции}
writeln (x:10:2, y:10:2);
{печать строки таблицы}
x:=x+0.25; {шаг по x}
end;
end.
"Расширим" задачу за счет использования произвольных границ изменения аргумента и произвольного шага, а также выполнения всех необходимых проверок корректности. Пусть, например, требуется составить таблицу значений следующей функции:
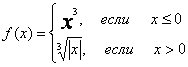, значения
a, b вводятся пользователем.
Напишем текст программы, сопроводив его соответствующими комментариями.
var x,f,a,b,dx:real;
n:integer; {счетчик выведенных строк}
begin
repeat {Цикл ввода с контролем
правильности значений: a,dx,b должны быть
числами, dx>0, a+dx должно быть меньше b}
writeln ('Введите a,dx,b:');
{$I-}read (a,dx,b);{$I+}
if IoResult <> 0 then begin
writeln ('Вы не ввели 3 числовых ',
'значения, попробуем еще раз');
continue;
end;
if (dx<=0) or (a+dx>=b) then begin
writeln ('Вы не ввели допустимые ',
'данные, попробуем еще раз');
continue;
end
else break;
until false;
{Печать заголовка таблицы}
writeln;
writeln ('x':10,'f(x)':10);
x:=a;
n:=2; {2 строки уже использованы}
while x<=b+1e-6 do begin
{в условии цикла учитываем возможную
погрешность работы с real!}
if x<=0 then f:=sqr(x)*x
else f:=exp(1/3*ln(abs(x)));
{корень 3 степени взяли через exp и ln}
writeln (x:10:2,f:10:2);
n:=n+1;
if n=24 then begin
{На экране консоли по умолчанию 25 строк}
write ('Нажмите Enter...');
reset (input); readln;
n:=1;
end;
x:=x+dx;
end;
writeln ('Таблица выведена');
reset (input); readln;
end.
Как видно из примера, основной порядок действий -- такой же, как в предыдущей задаче. Так как экран консоли по умолчанию содержит всего 25 строк, с помощью переменной n мы дополнительно контролируем число уже выведенных строк и делаем по заполнении экрана паузу до нажатия пользователем клавиши Enter.
Разумеется, другие изученные нами виды циклов также могут применяться при табулировании. Рассмотрим в качестве примера следующую задачу.
Известна стоимость единицы товара. Составить таблицу стоимости 1, 2, ..., K единиц товара, значение K вводится.
Так как число единиц товара -- заведомо целое, при программировании задачи будет удобен цикл for:
var t:real;
i,k:integer;
begin
writeln;
writeln ('Стоимость единицы товара:');
read (t);
writeln ('Количество единиц товара:');
read (k);
writeln ('Единиц':10,'Стоимость':10);
for i:=1 to k do
writeln (i:10,(i*t):10:2);
end.
Здесь для простоты мы исключили сделанные в предыдущем примере проверки. Стоимость единицы товара обозначена t, переменная i необходима для перебора возможных значений единиц товара в цикле for. Поскольку счетчик цикла for автоматически меняется с шагом 1, а оператором writeln можно выводить не только значения переменных, но и выражения, основной цикл программы состоит из одного оператора и не нуждается в операторных скобках.
Этот алгоритм применяется, когда требуется подсчитать количество элементов данных, отвечающих какому-либо условию или условиям. В общем виде алгоритм описывается следующим образом:
1. в разделе var описать переменную целочисленного типа, с помощью которой будет вестись подсчет;
2. до цикла присвоить ей начальное значение 0;
3. в теле цикла, если очередной элемент данных отвечает условию подсчета, увеличить эту переменную на 1 оператором вида k:=k+1;.
Необходимость присваивания начальных значений на шаге 2 этого и последующих алгоритмов связана с тем, что после описания в разделе var значение переменной еще не определено. "Пока мы не начали подсчитывать количество, оно равно нулю" -- этот очевидный для человека факт не очевиден для компьютера! Поэтому любой переменной, которая может изменяться в теле цикла, необходимо присвоить до цикла начальное значение, что и делает оператор вида k:=0;.
Рассматриваемый нами алгоритм очень часто встречается в самых различных задачах, поэтому для "быстрой" записи операции по увеличению счетчика (она называется инкремент) или его уменьшению (декремент) существуют специальные стандартные процедуры:
Inc(X,N); -- увеличивает значение переменной.
Здесь параметр X -- переменная порядкового типа, а N -- переменная или выражение целочисленного типа. Значение X увеличивается на 1, если параметр N не определен, или на N, если параметр N определен, то есть Inc(X); соответствует X:=X+1;, а Inc(X,N); соответствует X:=X+N;.
Dec(X,N); -- уменьшает значение переменной.
Параметр X -- также переменная порядкового типа, N -- целочисленное значение или выражение. Значение X уменьшается на 1, если параметр N не определен, или на N, если параметр N определен, то есть Dec(X); соответствует X:=X-1;, а Dec(X,N); соответствует X:=X-N;.
С помощью Inc и Dec генерируется более оптимизированный код, особенно полезный в сложных циклах. Возможно, мы будем использовать их не во всех примерах, но вам советую о них не забывать.
В качестве примера реализации алгоритма рассмотрим следующую задачу.
Последовательность z(i) задана
соотношениями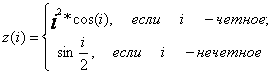 
,
i=1,2,...,100. Найти количество элементов последовательности,
больших значения 0.5.
Обозначив искомое количество за k, составим программу:
var z:real;
i,k:integer;
begin
k:=0;
for i:=1 to 100 do begin
if i mod 2 = 0 then z:=sqr(i)*cos(i)
else z:=sin(i/2);
if z>0.5 then inc(k);
end;
writeln ('Количество=',k);
end.
Так как шаг по переменной i равен 1, в программе использован цикл for, для проверки того, является ли значение i четным, использована операция mod.
В следующей задаче займемся обработкой данных по мере их ввода пользователем.
Известны оценки за экзамен по информатике для группы из n студентов, 2≤n≤25. Оценить количественную и качественную успеваемость группы по формулам:
, 
, где k1 -- количество
"троек", "четверок" и "пятерок", k2 --
количество только "четверок" и "пятерок".
Для ввода текущей оценки используем целочисленную переменную a, в качестве счетчика цикла for введем переменную i ("номер студента"), остальные величины описаны в условии задачи. При вводе значения n и очередного значения a для простоты не будем контролировать корректность вводимых данных.
var a,i,n,k1,k2:integer;
ykol,ykach:real;
begin
writeln;
writeln ('Введите количество студентов:');
read (n);
k1:=0;
k2:=0;
for i:=1 to n do begin
write ('Введите оценку ',i,' студента:');
read (a);
if a>2 then begin
inc(k1);
if a>3 then inc(k2);
end;
end;
ykol:=k1/n*100;
ykach:=k2/n*100;
writeln
('Количественная успеваемость=',ykol:6:2);
writeln
('Качественная успеваемость =',ykach:6:2);
reset (input); readln;
end.
Данные алгоритмы применяются, когда требуется сложить или перемножить выбранные данные. В общем виде эти широко применяемые алгоритмы можно описать так:
1. для подсчета каждой суммы или произведения описать по одной переменной того же типа, что суммируемые или перемножаемые данные;
2. до цикла переменной-сумме присвоить начальное значение 0, а произведению -- значение 1;
3. в теле цикла, если очередной элемент данных t отвечает условию суммирования или перемножения, сумма накапливается оператором вида s:=s+t;, а произведение -- оператором вида p:=p*t;
Очевидно, почему начальное значение произведения -- 1, а не 0. После оператора p:=0; оператор p:=p*t;, расположенный в теле цикла, будет возвращать только нули.
Рассмотрим типовую задачу. Для функции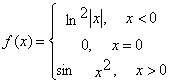 
, 
найти арифметическое среднее ее положительных
значений и произведение ненулевых значений.
Для поиска арифметического среднего необходимо сначала найти сумму s и количество k положительных значений функции. Составим следующую программу:
var x,f,s,p:real;
k:integer;
begin
s:=0; k:=0; p:=1;
x:=-5;
while x<=5+1e-6 do begin
if x<0 then f:=sqr(ln(abs(x)))
else if x>0 then f:=sin(sqr(x))
else f:=0;
if f>0 then begin
s:=s+f;
k:=k+1;
end;
if f<>0 then p:=p*f;
x:=x+0.5;
end;
s:=s/k; {теперь в s - искомое среднее}
writeln
('Среднее положительных =',s:10:6);
writeln
('Произведение ненулевых=',p:10:6);
reset (input); readln;
end.
В следующей задаче также применяется алгоритм накопления суммы.
Требуется написать программу, имитирующую работу кассового аппарата: пользователь в цикле вводит цену очередного товара или 0 для завершения ввода, программа суммирует цены. По завершении цикла ввода программа начисляет скидку с общей стоимости товара по правилам: скидки нет, если общая стоимость покупки -- менее 10000 руб.; скидка равна 5%, если общая стоимость -- от 10000 до 20000 руб.; скидка равна 7%, если общая стоимость -- свыше 20000 руб. После начисления скидки выводится окончательная стоимость покупки.
Обозначив общую стоимость покупки s, а цену очередного товара -- t, напишем следующую программу:
var s,t:real;
begin
writeln;
s:=0; {начальное значение суммы!}
repeat
writeln ('Введите стоимость товара или '
'0 для завершения ввода:');
{$I-}read(t);{$I+}
if (IoResult<>0) or (t<0) then begin
writeln ('Ошибка! Повторите ввод');
continue;
end;
if t=0 then break;
{Округляем t до 2 знаков после запятой -
на случай, если есть копейки}
t:=round (t*100) / 100;
s:=s+t; {накопление суммы}
until false;
{Начисление скидки и вывод ответа}
writeln ('Стоимость без скидки:',s:8:2);
if s>20000 then s:=s-s*0.07
else if s>10000 then s:=s-s*0.05;
writeln ('Стоимость со скидкой:',s:8:2);
writeln ('Спасибо за покупку!');
reset (input); readln;
end.
Тип данных real выбран для s и t не случайно -- выбор integer ограничил бы диапазон обрабатываемых значений и не позволил в удобном виде ввести копейки. Проверки корректности ввода, делаемые программой, знакомы по предыдущим примерам и поэтому не закомментированы.
 гостевая; E-mail
|
