|
Pers.narod.ru. Обучение. Лекции по численным методам. Аппроксимация и интерполяция функций |
Локальная интерполяция:
Кусочно–постоянная интерполяция
Кусочно–линейная интерполяция
Кубический интерполяционный сплайн
Глобальная интерполяция:
Полином Лагранжа
Подбор эмпирических формул
Метод наименьших квадратов
Аппроксимировать – это означает "приближённо заменять". Допустим, известны значения некоторой функции в заданных точках. Требуется найти промежуточные значения этой функции. Это так называемая задача о восстановлении функции. Кроме того, при проведении расчетов сложные функции удобно заменять алгебраическими многочленами или другими элементарными функциями, которые достаточно просто вычисляются (задача о приближении функции).
На интервале
[a, b] заданы точки xi,
i=0, 1,..., N; a ≤ x i ≤ b, и значения неизвестной функции в
этих точках fi, i=0, 1,...., N. Требуется найти функцию F(x), принимающую в точках xi те же значения fi. Точки ![]() называются узлами
интерполяции, а условия F(xi)=
fi. – условиями интерполяции. При этом F(x)
ищем только на отрезке [a,b]. Если необходимо найти функцию вне отрезка, то -
это задача экстраполяции. Пока мы будем рассматривать только интерполяционные задачи.
называются узлами
интерполяции, а условия F(xi)=
fi. – условиями интерполяции. При этом F(x)
ищем только на отрезке [a,b]. Если необходимо найти функцию вне отрезка, то -
это задача экстраполяции. Пока мы будем рассматривать только интерполяционные задачи.
Задача имеет
много решений, т.к. через заданные точки (xi, fi),
i=0, 1,..., N, можно провести
бесконечно много кривых, каждая из которых будет графиком функции, для которой
выполнены все условия интерполяции. Для практики важен случай аппроксимации
функции многочленами, т.е. ![]() .
.
Все методы интерполяции можно разделить на локальные и глобальные. В случае локальной интерполяции на каждом интервале [xi–1, xi] строится отдельный полином. В случае глобальной интерполяции отыскивается единый полином на всем интервале [a, b]. При этом искомый полином называется интерполяционным полиномом.
На каждом
отрезке ![]() интерполяционный
многочлен равен константе, а именно левому или правому значению функции.
интерполяционный
многочлен равен константе, а именно левому или правому значению функции.
Для левой кусочно-линейной
интерполяции ![]() ,
т.е.
,
т.е.
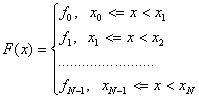
Для правой кусочно-линейной
интерполяции ![]() ,
т.е.
,
т.е.
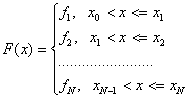
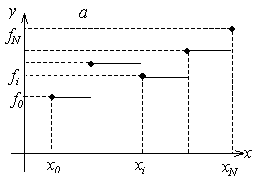
Легко понять, что условия интерполяция выполняются. Построенная функция является разрывной), что ограничивает ее применение. Для левой кусочно-линейной интерполяции имеем графическое представление:
На каждом интервале
[xi–1, xi] функция является линейной ![]() . Значения коэффициентов
находятся из выполнения условий интерполяции в концах отрезка:
. Значения коэффициентов
находятся из выполнения условий интерполяции в концах отрезка: ![]() . Получаем систему уравнений:
. Получаем систему уравнений:
![]() , откуда
находим
, откуда
находим ![]()
![]() .
Следовательно, функцию F(z)
можно записать в виде:
.
Следовательно, функцию F(z)
можно записать в виде:
![]() , т.е.
, т.е.
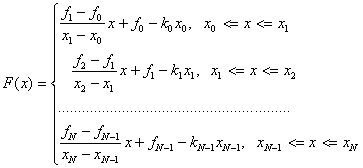
Или
F(x) = ki * (x - xi-1) + fi-1,
ki = (fi - fi-1) / (xi - xi-1), xi-1 ≤ x ≤ xi, i=1,2,...,N-1
При использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение x, а затем подставить его в формулу.
Итоговая функция будет непрерывной, но производная будет разрывной в каждом узле интерполяции. Погрешность такой интерполяции будет меньше, чем в случае кусочно–постоянной интерполяции. Иллюстрация кусочно–линейной интерполяции приведена на рисунке
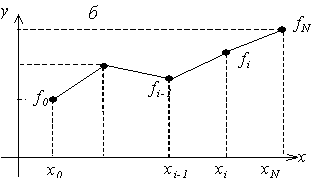
Пример: Заданы значений некоторой функции:
| x | 0 | 2 | 3 | 3.5 |
| f | -1 | 0.2 | 0.5 | 0.8 |
Требуется найти значение функции при z=1 и z=3.2 по кусочно–постоянной и кусочно–линейной интерполяции.
Решение.
Точка z=1 принадлежит первому локальному
отрезку [0, 2], т.е. ![]() и, следовательно, по формулам левой кусочно–постоянной
интерполяции F(1) = f0 = –1, по формулам правой кусочно–постоянной
интерполяции F(1)=f1=0.2.
Воспользуемся формулами кусочно–линейной интерполяции:
и, следовательно, по формулам левой кусочно–постоянной
интерполяции F(1) = f0 = –1, по формулам правой кусочно–постоянной
интерполяции F(1)=f1=0.2.
Воспользуемся формулами кусочно–линейной интерполяции:
![]()
![]() .
.
Точка z=3.2 принадлежит третьему интервалу [3, 3.5], т.е. ![]() и, следовательно, по
формулам левой кусочно – постоянной интерполяции F(3.2)=
и, следовательно, по
формулам левой кусочно – постоянной интерполяции F(3.2)=![]() =0.5, по формулам правой кусочно
– постоянной интерполяции F(3.2)=
=0.5, по формулам правой кусочно
– постоянной интерполяции F(3.2)= 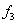 =0.8. Воспользуемся формулами кусочно–линейной
интерполяции:
=0.8. Воспользуемся формулами кусочно–линейной
интерполяции:
![]()
![]()
Слово сплайн (английское слово "spline") означает гибкую линейку, используемую для проведения гладких кривых через заданные точки на плоскости. Форма этого универсального лекала на каждом отрезке описывается кубической параболой. Сплайны широко используются в инженерных приложениях, в частности, в компьютерной графике. Итак, на каждом i–м отрезке [xi–1, xi], i=1, 2,…, N, решение будем искать в виде полинома третьей степени:
Si(x)=ai+bi(x–xi)+ci(x–xi)2/2+di(x–xi)3/6
Неизвестные коэффициенты ai, bi, ci, di, i=1, 2,..., N, находим из:
• условий интерполяции: Si(xi)=fi, i=1, 2,..., N; S1(x0)=f0,
• непрерывности функции Si(xi–1)=Si–1(xi–1), i=2, 3,..., N,
• непрерывности первой и второй производной:
S /i(xi–1)=S /i–1(xi–1), S //i(xi–1)=S //i–1(x i–1), i=2, 3,..., N.
Учитывая, что ![]() , для определения 4N неизвестных
получаем систему 4N–2 уравнений:
, для определения 4N неизвестных
получаем систему 4N–2 уравнений:
ai=fi, i=1, 2,..., N,
bi hi – cihi2/2 + di hi3/6=fi – fi–1, i=1, 2,..., N,
bi – bi–1 = ci hi – di hi2/2, i=2, 3,..., N,
di hi = ci – ci–1 , i=2, 3,..., N.
где hi=xi
– xi–1. Недостающие два уравнения выводятся из
дополнительных условий: S //(a)=S //(b)=0.
Можно показать, что при этом ![]() . Из системы можно исключить
неизвестные bi , di , получив систему N+1 линейных уравнений (СЛАУ) для определения
коэффициентов ci:
. Из системы можно исключить
неизвестные bi , di , получив систему N+1 линейных уравнений (СЛАУ) для определения
коэффициентов ci:
c0 =0, cN =0,
hici–1+2(hi+hi+1)ci+h
i+1ci+1=6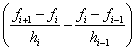 , i=1, 2,…, N–1. (1)
, i=1, 2,…, N–1. (1)
После этого вычисляются коэффициенты bi, di:
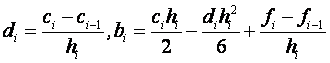 , i=1, 2,..., N. (2)
, i=1, 2,..., N. (2)
В случае постоянной сетки hi=h эта система уравнений упрощается.
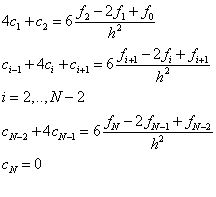
Данная CЛАУ имеет трехдиагональную матрицу и решается методом прогонки.
Коэффициенты 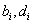 определяются из формул:
определяются из формул:
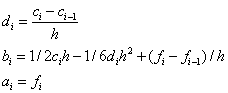
Для вычисления значения S(x) в произвольной точке отрезка z∈[a, b] необходимо решить систему уравнений на коэффициенты ci, i=1,2,…, N–1, затем найти все коэффициенты bi, di. Далее, необходимо определить, на какой интервал [xi0, xi0–1] попадает эта точка, и, зная номер i0, вычислить значение сплайна и его производных в точке z
S(z)=ai0 +bi0(z–xi0)+ci0(z–xi0)2/2+di0(z–x i0)3/6
S /(z)=bi0+ci0(z–xi0)+di0(z–x i0)2/2, S //(z)=ci0+di0(z–x i0).
Пример.
|
|
x0,f0 |
x1,f1 |
x2,f2 |
x3,f3 |
x4,f4 |
|
х |
0 |
¼ |
1/2 |
3/4 |
1 |
|
f |
1 |
2 |
1 |
0 |
1 |
Требуется вычислить значения функции в точках 0.25 и 0.8, используя сплайн – интерполяцию.
В нашем случае: hi=1/4,
![]() .
.
Выпишем систему уравнений для
определения ![]() :
:
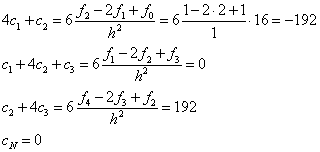
Решая эту систему линейных
уравнений, получим: ![]() .
.
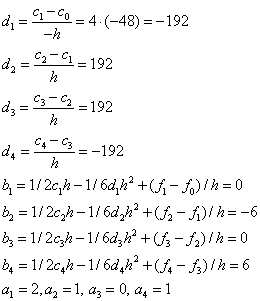
Рассмотрим точку 0.25, которая
принадлежит первому отрезку, т.е. ![]() . Следовательно, получим,
. Следовательно, получим, 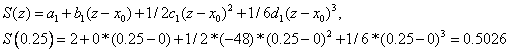
Рассмотрим точку 0.8, которая
принадлежит четвертому отрезку, т.е. ![]() .
.
Следовательно, 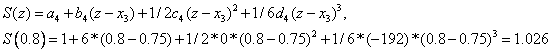
В случае глобальной интерполяции отыскивается единый полином на всем интервале [a, b], т.е. строится полином, который используется для интерполяции функции f(x) на всем интервале изменения аргумента x. Будем искать интерполирующую функцию в виде полинома (многочлена) m–ой степени Pm(x)=a0+a1x+a2x2+a3x3+…+am xm. Какова должна быть степень многочлена, чтобы удовлетворить всем условиям интерполяции? Допустим, что заданы две точки: (x0, f0) и (x1, f1), т.е. N=1. Через эти точки можно провести единственную прямую, т.е. интерполирующей функцией будет полином первой степени P1(x)=a0+a1x. Через три точки (N=2) можно провести параболу P2(x)=a0+a1x+a2x2 и т.д. Рассуждая таким способом, можно предположить, что искомый полином должен иметь степень N .
Для того, чтобы доказать это, выпишем систему уравнений на коэффициенты. Уравнения системы представляют собой условия интерполяции в при каждом x=xi:
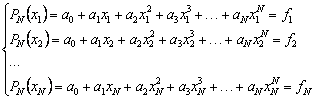
Данная система является линейной относительно искомых коэффициентов a0, a1, a2,…, aN. Известно, что СЛАУ имеет решение, если ее определитель отличен от нуля. Определитель данной системы
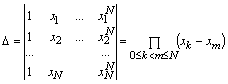
носит имя определителя Вандермонда. Из курса математического анализа известно, что он отличен от нуля, если xk≠ xm (т.е. все узлы интерполяции различные). Таким образом, доказано, что система имеет решение.
Мы показали,
что для нахождения коэффициентов
a0, a1,
a2,…, aN надо решить СЛАУ, что является сложной задачей.
Но есть другой способ построения полинома N–й
степени, который не требует решения такой системы.
Решение ищем в
виде ![]() ,
где li(z) – базисные
полиномы N–й степени, для которых выполняется
условие:
,
где li(z) – базисные
полиномы N–й степени, для которых выполняется
условие: ![]() .
Убедимся в том, что если такие полиномы построены, то LN(x) будет удовлетворять условиям интерполяции:
.
Убедимся в том, что если такие полиномы построены, то LN(x) будет удовлетворять условиям интерполяции:
![]() .
.
Каким образом построить базисные полиномы? Определим
![]() , i=0, 1,..., N.
, i=0, 1,..., N.
Легко понять, что
Функция li(z) является полиномом N–й степени от z и для нее выполняются условия "базисности":
![]() =0, i≠k;, т.е. k=1,…,i-1
или k=i+1,…,N.
=0, i≠k;, т.е. k=1,…,i-1
или k=i+1,…,N.
![]() .
.
Таким образом,
нам удалось решить задачу о построении интерполирующего полинома N– й степени, и для этого не нужно решать СЛАУ. Полином
Лагранжа можно записать в виде компактной формулы: 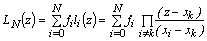 . Погрешность этой формулы можно
оценить, если исходная функция g(x) имеет производные до N+1
порядка:
. Погрешность этой формулы можно
оценить, если исходная функция g(x) имеет производные до N+1
порядка:
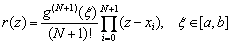 .
.
Из этой формулы следует, что погрешность метода зависит от свойств функции g(x), а также от расположения узлов интерполяции и точки z. Как показывают расчетные эксперименты, полином Лагранжа имеет малую погрешность при небольших значениях N<20. При бόльших N погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (т.е. его погрешность не убывает с ростом N).
Рассмотрим частные случаи. Пусть N=1, т.е. заданы значения функции только в двух точках. Тогда базовые полиномы имеют вид:
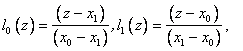
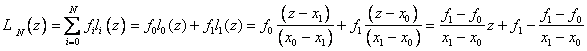 , т.е. получаем формулы кусочно–линейной
интерполяции.
, т.е. получаем формулы кусочно–линейной
интерполяции.
Пусть N=2. Тогда: 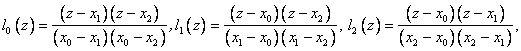
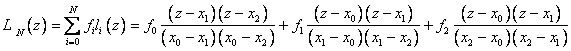
В результате мы получили формулы так называемой квадратичной или параболической интерполяции.
Пример: Заданы значений некоторой функции:
| x | 0 | 2 | 3 | 3.5 |
| f | -1 | 0.2 | 0.5 | 0.8 |
Требуется найти значение функции при z=1, используя интерполяционный полином Лгранжа. Для этого случая N=3, т.е. полином Лагранжа имеет третий порядок. Вычислим значения базисных полиномов при z=1:
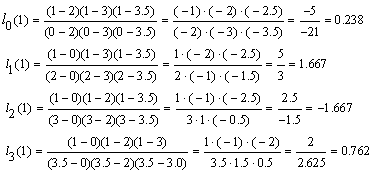
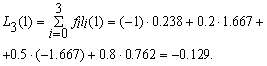
При
интерполировании функций мы использовали условие равенства значений
интерполяционного полинома и данной функции в узлах интерполяции. Если же
исходные данные получены в результате опытных измерений, то требование точного
совпадения не нужно, так как данные не получены точно. В этих случаях можно
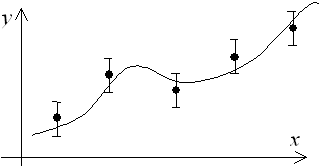
требовать лишь приближенного выполнения условий интерполяции ![]() . Это условие означает,
что интерполирующая функция F(x) проходит не точно через заданные точки, а в некоторой их окрестности, так, например, как это показано
на рис.
. Это условие означает,
что интерполирующая функция F(x) проходит не точно через заданные точки, а в некоторой их окрестности, так, например, как это показано
на рис.
Тогда говорят
о подборе эмпирических формул. Построение эмпирической формулы состоит
из двух этапов6 подбора вида этой формулы ![]() , содержащей неизвестные параметры
, содержащей неизвестные параметры ![]() , и определение наилучших в
некотором смысле этих параметров. Вид формулы иногда известен из физических
соображений (для упругой среды связь между напряжением и деформацией) или
выбираются из геометрических соображений: экспериментальные точки наносятся на график
и примерно угадывается общий вид зависимости путем сравнения полученной кривой
с графиками извесиных функций. Успех здесь в значительной степени определяется
опытом и интуицией исследователя.
, и определение наилучших в
некотором смысле этих параметров. Вид формулы иногда известен из физических
соображений (для упругой среды связь между напряжением и деформацией) или
выбираются из геометрических соображений: экспериментальные точки наносятся на график
и примерно угадывается общий вид зависимости путем сравнения полученной кривой
с графиками извесиных функций. Успех здесь в значительной степени определяется
опытом и интуицией исследователя.
Для практики
важен случай аппроксимации функции многочленами, т.е. 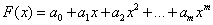 .
.
После того, как выбран вид эмпирической зависимости степень близости к эмпирическим данным определяется, используя минимум суммы квадратов отклонений вычисленных и экспериментальных данных.
Пусть для
исходных данных xi, fi, i=1,…,N (нумерацию лучше начинать с единицы), выбран вид эмпирической
зависимости: ![]() с
неизвестными коэффициентами
с
неизвестными коэффициентами ![]() . Запишем сумму квадратов отклонений между
вычисленными по эмпирической формуле и заданными опытными данными:
. Запишем сумму квадратов отклонений между
вычисленными по эмпирической формуле и заданными опытными данными:
![]() .
.
Параметры ![]() будем находить из условия
минимума функции
будем находить из условия
минимума функции ![]() .
В этом состоит метод наименьших квадратов (МНК).
.
В этом состоит метод наименьших квадратов (МНК).
Известно, что
в точке минимума все частные производные от ![]() по
по ![]() равны нулю:
равны нулю:
![]() (1)
(1)
Рассмотрим применение МНК для частного случая, широко используемого на практике. В качестве эмпирической функции рассмотрим полином
![]()
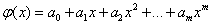 .
.
Формула (1) для определения суммы квадратов отклонений примет вид:
![]() (2)
(2)
Вычислим производные:

Приравнивая эти
выражения нулю и собирая коэффициенты при неизвестных 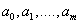 , получим следующую систему линейных
уравнений:
, получим следующую систему линейных
уравнений:

Данная система
уравнений называется нормальной. Решая эту систему линейных уравнений,
получаем коэффициенты ![]() .
.
В случае
полинома первого порядка m=1, т.е. 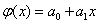 , система нормальных уравнений
примет вид:
, система нормальных уравнений
примет вид:

При m=2 имеем:

Как правило, выбирают несколько эмпирических зависимостей. По МНК находят коэффициенты этих зависимостей и среди них находят наилучшую по минимальной сумме отклонений.
Пример. Заданы координаты точек:
|
x |
-5 |
-3.5 |
-2 |
1.5 |
3.25 |
5 |
|
f |
0.5 |
1.2 |
1.4 |
1.6 |
1.7 |
1.5 |
т.е. N=6. Требуется найти эмпирические зависимости: линейную ![]() , квадратичную
, квадратичную ![]() , гиперболическую
, гиперболическую ![]() по методу МНК и выбрать среди
них наилучшую по наименьшей сумме квадратов отклонений.
по методу МНК и выбрать среди
них наилучшую по наименьшей сумме квадратов отклонений.
Система нормальных уравнений для линейной зависимости:

Учитывая, что N=6, ![]() ,
получим
,
получим
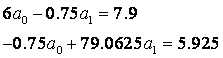
Решая систему
линейных уравнений, получим ![]() . Следовательно, линейная зависимость имеет
вид:
. Следовательно, линейная зависимость имеет
вид: ![]() .
.
Вычислим сумму
квадратов отклонений: ![]() .
.
Рассмотрим квадратичную зависимость. Система нормальных уравнений имеет вид
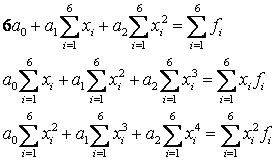
Найдем неподсчитанные
суммы: ![]()
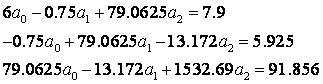
Решая СЛАУ,
получим ![]()
Следовательно,
квадратичная зависимость имеет вид: ![]() .
.
Вычислим сумму
квадратов отклонений: ![]() .
.
Выпишем систему нормальных уравнений для гиперболической зависимости. Согласно МНК находим сумму квадратов отклонений:
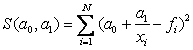 . Составляем систему
нормальных уравнений:
. Составляем систему
нормальных уравнений:

Или

Учитывая, что ![]() , получим
, получим
![]()
Сумма
квадратов отклонений:![]()
Из трех зависимостей выбираем наилучшую, т.е. квадратичную.
|
|