2. Методы решения систем линейных алгебраических уравнений

Прямые методы решения СЛАУ:
    Метод Крамера
    Метод обратной матрицы
    Метод Гаусса
Итерационные методы решения линейных алгебраических систем:
    Метод простой итерации или метод Якоби
    Метод Гаусса – Зейделя

К решению систем линейных алгебраических уравнений сводятся многочисленные практические задачи ( по некоторым оценкам более 75% всех задач). Можно с полным основанием утверждать, что решение линейных систем является одной из самых распространенных и важных задач вычислительной математики.

Конечно, существует много методов и современных пакетов прикладных программ для решения СЛАУ, но для того, чтобы их успешно использовать, необходимо разбираться в основах построения методов и алгоритмов, иметь представления о недостатках и преимуществах используемых методов.

Постановка задачи

Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как

,

Эту систему уравнений можно записать также в матричном виде:

,

где , , .

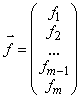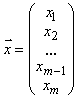A – матрица системы, – вектор правых частей, 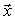– вектор неизвестных.

При известных A и 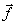требуется найти такие , при подстановке которых в систему уравнений она превращается в тождество.

Необходимым и достаточным условием существования единственного решения СЛАУ является условие det A≠0, т.е. определитель матрицы A не равен нулю. В случае равенства нулю определителя матрица A называется вырожденной и при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.

В дальнейшем будем предполагать наличие единственного решения.

Все методы решения линейных алгебраических задач можно разбить на два класса: прямые (точные) и итерационные (приближенные).

Прямые методы решения СЛАУ

Метод Крамера

При небольшой размерности системы m (m = 2,…,5) на практике часто используют формулы Крамера для решения СЛАУ:

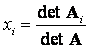(i = 1, 2, …, m). Эти формулы позволяют находить неизвестные в виде дробей, знаменателем которых является определитель матрицы системы, а числителем – определители матриц A_i, полученных из A заменой столбца коэффициентов при вычисляемом неизвестном столбцом свободных членов. Так А₁ получается из матрицы А заменой первого столбца на столбец правых частей f.

Например, для системы двух линейных уравнений

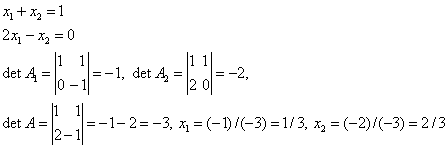
Размерность системы (т.е., число m) является главным фактором, из–за которого формулы Крамера не могут быть использованы для численного решения СЛАУ большого порядка. При непосредственном раскрытии определителей решение системы с m неизвестными требует порядка m!*m арифметических операций. Таким образом, для решения системы, например, из m = 100 уравнений потребуется совершить 10¹⁵⁸ вычислительных операций (процесс займёт примерно 10¹⁹ лет), что не под силу даже самым мощным современным ЭВМ

Метод обратной матрицы

Если det A ≠ 0, то существует обратная матрица . Тогда решение СЛАУ записывается в виде: . Следовательно, решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы. Проблемы использования этого метода те же, что и при использовании метода Крамера: нахождение обратной матрицы – трудоемкая операция.

Метод Гаусса

Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений

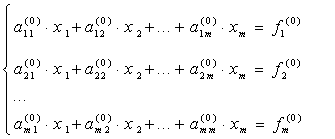
первый элемент . Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на и исключим x₁ из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при в соответствующей строке. Получим

.

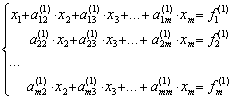Если , то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей

.

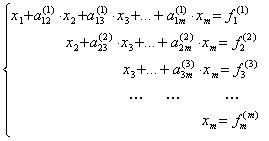Из нее в обратном порядке находим все значения x_i:

.

Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных – обратным. В случае если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие–либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных добиваются выполнения условия:

, j = i+1,i+ 2, …, m;

т.е. осуществляется выбор первого главного элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a₁₁ был максимальным по модулю. Разделив первую строку на главный элемент, как и прежде, исключают x₁ из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.

Рассмотрим применение метода Гаусса с выбором главного элемента на примере следующей системы уравнений:

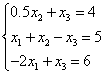
В первом уравнении коэффициент при =0, во втором = 1 и в третьем = -2, т.е. максимальный по модулю коэффициент в третьем уравнении. Поэтому переставим третье и первое уравнение:

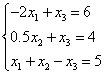
Исключим из второго и третьего уравнений с помощью первого. Во втором уравнении исключать не надо. Для исключения из третьего уравнения умножим первое на 0.5 и сложим с третьим:

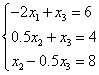
Рассмотрим второе и третье уравнения. Максимальный по модулю элемент при в третьем. Поэтому поместим его на место второго:

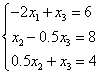
Исключим из третьего уравнения. Для этого умножим второе на -0.5 и сложим с третьим:

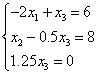
Обратный ход: .

Проверка: 0.5*8+0=4, -3+8-0=5, -2*(-3)+0=6.

Такая перестановка уравнений необходима для того, чтобы уменьшить влияние ошибок округления на конечный результат.

Часто возникает необходимость в решении СЛАУ, матрицы которые являются слабо заполненными, т.е. содержат много нулевых элементов. В то же время эти матрицы имеют определенную структуру. Среди таких систем выделим системы с матрицами ленточной структуры, в которых ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов вместо метода Гаусса можно использовать более эффективные методы. Например, метод прогонки, который мы рассмотрим позже при решении краевой задачи для обыкновенного дифференциального уравнения второго порядка.

Итерационные методы решения линейных алгебраических систем

Метод простой итерации или метод Якоби

Напомним, что нам требуется решить систему линейных уравнений, которая в матричном виде записывается как:

,

где , , .

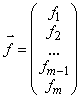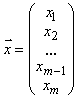Предположим, что диагональные элементы матриц A исходной системы не равны 0 (a_ii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно x₁, второе относительно x₂ и т.д. Получим следующую эквивалентную систему, записанную в скалярном виде:

(1),

Теперь, задав нулевое приближение , по рекуррентным соотношениям (1) можем выполнять итерационный процесс, а именно:

Аналогично находятся следующие приближения , где в (2) вместо 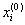необходимо подставить .

Или в общем случае:

. (3)

или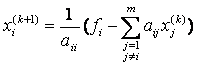

Условие окончания итерационного процесса .

Достаточное условие сходимости: Если выполнено условие диагонального преобладания, т.е. 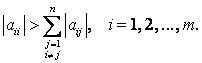, то итерационный процесс (3) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.

Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут или .

Замечание. Указанное выше условие сходимости является достаточным, т.е. если оно выполняется, то процесс сходится. Однако процесс может сходиться и при отсутствии диагонального преобладания, а может и не сойтись.

Пример.

Решить систему линейных уравнений с точностью :

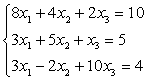
	8	4	2		10		x1
=	3	5	1	=	5	=	x2
	3	–2	10		4		x3

Решение прямыми методами, например, обратной матрицей, даёт решение:

.

Найдем решение методом простой итерации. Проверяем условие диагонального преобладания: , , .

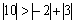Приводим систему уравнений к виду (1):

.

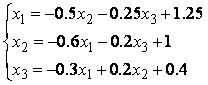Начальное приближение . Дальнейшие вычисления оформим в виде таблицы:

Здесь

,

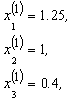
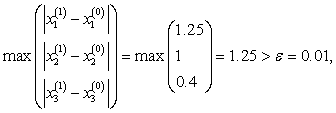
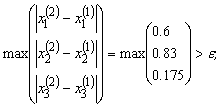
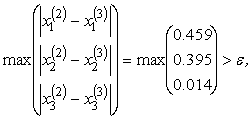
И т.д., пока не получим, в последнем столбце величину меньшую 0.01, что произойдет на 13 – ой итерации.

Следовательно, приближенное решение имеет вид:

Метод Гаусса – Зейделя

Расчетные формулы имеют вид:

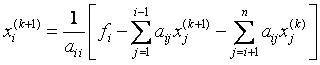
т.е. для подсчета i–й компоненты (k+1)–го приближения к искомому вектору используется уже вычисленное на этом, т.е. (k+1)–м шаге, новые значения первых i–1 компонент.

Подробные формулы имеют вид:

Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:

Начальное приближение:

Найдем решение предыдущей системы уравнений методом Гаусса – Зейделя.

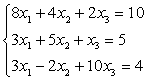
Расчетные формулы:

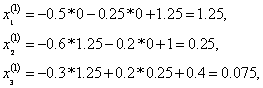
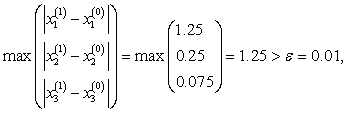
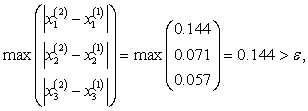
Из таблицы видно, что нужная точность достигнута уже на 5–ой итерации вместо 13–ой по методу простой итерации и значения корней более близки к значениям, полученным методом обратной матрицы.

гостевая; E-mail