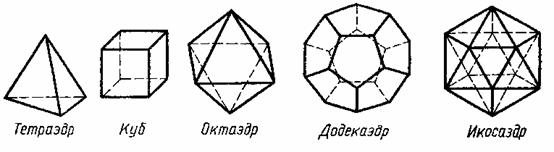
Для того, чтобы получить правильный многогранник, согласно его определению, в каждой вершине должно сходиться одинаковое количество граней, каждая из которых является правильным многоугольником. Сумма плоских углов многогранного угла должна быть меньше 360 градусов, иначе многогранной поверхности не получится. Перебирая возможные целые решения неравенств:

 60*k < 360
 90*k < 360 
108*k < 360 

можно доказать, что правильных многогранников - ровно пять (здесь k обозначает число плоских углов, сходящихся в одной вершине многогранника).

Названия "тетраэдр", "гексаэдр", "октаэдр", "додекаэдр", "икосаэдр" на греческом дословно означают "четырехгранник", "шестигранник", "восьмигранник", "двенадцатигранник", "двадцатигранник".

Для построения многогранников в Mathcad есть функция Polyhedron. Её можно использовать двумя способами:

• с аргументом по имени, тогда обращение к функции будет иметь вид Polyhedron("имя многогранника");
• с аргументом по коду, тогда обращение к функции будет иметь вид Polyhedron("#номер многогранника").

Вообще, аргумент функции Polyhedron может принимать значения от 1 до 80 включительно с предшествующим знаком "диез" (#), так что она умеет строить не только правильные многогранники, но и правильные невыпуклые многогранники и прочие звёздчатые формы.

Возможно, не все из этих штуковин ещё имеют имена, спешите увековечить своё, вдруг какой-нибудь дельтоидальный икоситетраэдр да ещё не назван :)

Здесь нет нормальной сводки формул для площадей и объёмов правильных многогранников (зато есть красивые анимации для них), а сводка формул имеется в приложенном документе MathCAD (формат .xmcd), вот его фрагмент

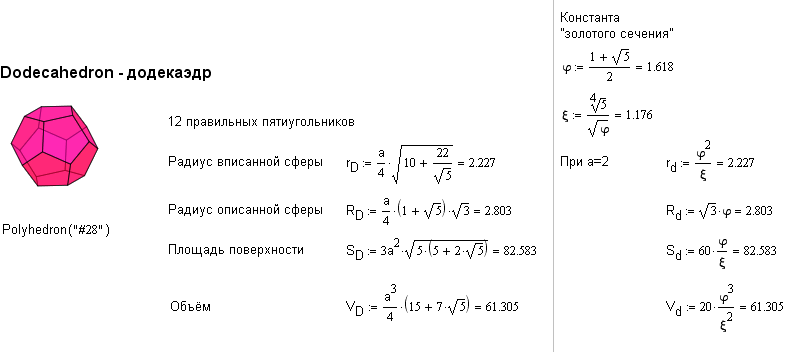
Только для додекаэдра и икосаэдра при длине ребра многоугольника a=2 или a=1 можно выразить основные формулы через константу "золотого сечения".

 Правильные многогранники в MathCAD (259 Кб)

гостевая; E-mail