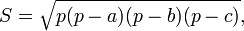
Pers.narod.ru. Алгоритмы. Площадь треугольника по длинам сторон (формула Герона) и координатам вершин |
Если треугольник задан длинами сторон a, b, c, его площадь может быть определена по формуле Герона:
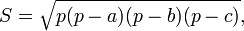
где p - полупериметр треугольника:
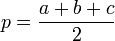
В приведённой ниже программе проверка существования треугольника с длинами сторон a, b, c не делается, её можно выполнить, например, вот так.
var a,b,c,p,s:real;
begin
write ('Введите стороны треугольника a,b,c:');
read (a,b,c);
p:=(a+b+c)/2;
s:=sqrt(p*(p-a)*(p-b)*(p-c));
write ('Площадь=',s:8:2);
reset (input); readln;
end.
Если треугольник задан координатами вершин (x1,y1), (x2,y2), (x3,y3), его площадь можно найти по формуле
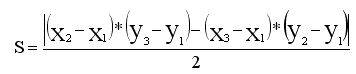
Вот соответствующая программа:
var x1,y1,x2,y2,x3,y3,s:real;
begin
write ('Введите координаты 1 вершины');
read (x1,y1);
write ('Введите координаты 2 вершины');
read (x2,y2);
write ('Введите координаты 3 вершины');
read (x3,y3);
s:=abs((x2-x1)*(y3-y1)-(x3-x1)*(y2-y1))/2;
write ('Площадь=',s:8:2);
reset (input); readln;
end.
|
|