Дано натуральное число N и действительные числа {Xi,Yi}, i=1,2,...,N, описывающие координаты вершин многоугольника на плоскости. Найти площадь выпуклого N-угольника, вершины которого при последовательном обходе имеют координаты {X1,Y1}, ..., {XN,YN}.

Алгоритм сводится к разбиению многоугольника на треугольники с общей вершиной в точке {X1,Y1} и последующим вычислением их площадей по форумле Герона.

Проверка того, действительно ли можно из введённых координат получить выпуклый многоугольник, не делается.

const nmax=10;
var x,y:array [1..nmax] of real;
 n,i:integer;
 s,r1,r2,r3,p,p2:real;
 
begin
 {Ввод данных}
 repeat
  write ('Число вершин (от 3 до ',nmax,'): ');
  {$I-}read (n);{$I+}
  if IoResult<>0 then continue;
 until (n>2) and (n<=nmax);
 for i:=1 to n do
 repeat
  write ('Координаты вершины ',i,': ');
  {$I-}read (x[i],y[i]);{$I+}
 until IoResult=0;
 {Реализация}
 s:=0;
 r1:=sqrt(sqr(x[1]-x[2])+sqr(y[1]-y[2]));
 for i:=3 to n do begin
  p:=r1;
  r2:=sqrt(sqr(x[i]-x[i-1])+sqr(y[i]-y[i-1]));
  p:=p+r2;
  r3:=sqrt(sqr(x[i]-x[1])+sqr(y[i]-y[1]));
  p:=p+r3;
  p2:=p/2;
  s:=s+sqrt(p2*(p2-r1)*(p2-r2)*(p2-r3));
  r1:=r3;
 end;
 {Вывод результата}
 writeln ('Площадь ',n,'-угольника=',s:8:2);
 write ('Нажмите Enter для выхода');
 reset (input); readln;
end.

Можно всё упростить, вычисляя площади треугольников через координаты их вершин.

const nmax=10;
var x,y:array [1..nmax] of real;
 n,i:integer;
 s:real;
 
begin
 {Ввод данных}
 repeat
  write ('Число вершин (от 3 до ',nmax,'): ');
  {$I-}read (n);{$I+}
  if IoResult<>0 then continue;
 until (n>2) and (n<=nmax);
 for i:=1 to n do
 repeat
  write ('Координаты вершины ',i,': ');
  {$I-}read (x[i],y[i]);{$I+}
 until IoResult=0;
 {Реализация}
 s:=0;
 for i:=1 to n-2 do
  s:=s+1/2*abs((x[i+1]-x[1])*(y[i+2]-y[1])-(x[i+2]-x[1])*(y[i+1]-y[1]));
 {Вывод результата}
 writeln ('Площадь ',n,'-угольника=',s:8:2);
 write ('Нажмите Enter для выхода');
 reset (input); readln;
end.

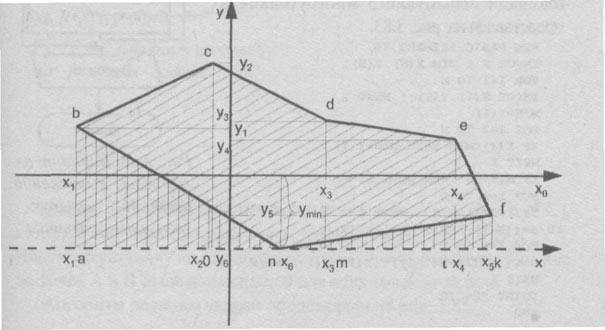
Теперь рассмотрим случай невыпуклого многоугольника, для которого столь простые алгоритмы неприменимы.

Примем, что многоугольник находится в области Y>0. Если это не так, его всегда можно переместить в положительную зону оси Y путём вычитания из всех координат Yi значения min{Yi}=Ymin. Общая площадь многоугольника будет равна сумме площадей прямоугольных трапеций, боковыми сторонами которых являются ось X и отрезок прямой, проведённый через 2 соседние вершины в порядке обхода. При этом в общей сумме площадь очередной трапеции учитывается со знаком "+", если значение Xi в последующей точке больше предыдущего в порядке обхода (наклонная штриховка на рисунке) или со знаком "-" в противном случае (вертикальная штриховка).

На нашем рисунке площади трапеций abco, ocdm, mdei и iefk будут учтены со знаком "+", так как X1<X2<X3<X4<X5, а площади треугольников nfk, nab, вычисляемые также по формуле прямоугольных трапеций, со знаком "-", так как X5>X6>X1.

const nmax=10;
var x,y:array [1..nmax] of real;
 n,i:integer;
 s,min:real;
 
begin
 {Ввод данных}
 repeat
  write ('Число вершин (от 3 до ',nmax,'): ');
  {$I-}read (n);{$I+}
  if IoResult<>0 then continue;
 until (n>2) and (n<=nmax);
 for i:=1 to n do
 repeat
  write ('Координаты вершины ',i,': ');
  {$I-}read (x[i],y[i]);{$I+}
 until IoResult=0;
 {Реализация}
 min:=y[1];
 for i:=2 to n do if y[i]<min then min:=y[i];
 if min<0 then for i:=1 to n do y[i]:=y[i]-min;
 s:=abs((x[1]-x[n])*(y[1]+y[n]))/2;
 for i:=2 to n do s:=s+abs((x[i]-x[i-1])*(y[i]+y[i-1]))/2;
 {Вывод результата}
 writeln ('Площадь ',n,'-угольника=',s:8:2);
 write ('Нажмите Enter для выхода');
 reset (input); readln;
end.

гостевая; E-mail