В литературе называется также методом касательных.

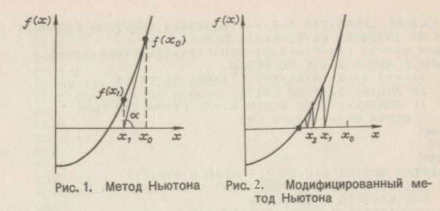
Рассмотрим графическую иллюстрацию метода (рис. 1). Предположим, что графическим методом определено начальное приближение х₀ к корню. В точке х₀ вычислим левую часть решаемого уравнения f₀ = f(x₀), а также производную в этой точке f'(x₀) = tg α. Следующее приближение к корню найдем в точке х₁, где касательная к функции f(x), проведенная из точки (х₀, f₀), пересекает ось абсцисс. Затем считаем точку х₁ в качестве начальной и продолжаем итерационный процесс. Из рис. видно, что таким способом можно приближаться к корню х*. При этом с каждой итерацией расстояние между очередным х_k+1 и предыдущим х_k приближениями к корню будет уменьшаться. Процесс уточнения корня закончим, когда выполнится условие

lx_{k + 1}- x_kl< e,

где е - допустимая погрешность определения корня.

Из геометрических соотношений (рис. 1) получим основную формулу метода Ньютона

x₁ = x₀ - f(x₀)/f'(x₀)

В общем виде для к-го шага итерационного процесса последнее соотношение принимает вид

x_k+1 = x_k - f(x_k)/f'(x_k)

Алгоритм Ньютона можно получить другим способом с помощью разложения в ряд Тейлора левой части уравнения f(x) вблизи корня х*. Пусть x_k+1=x_k+ s, тогда

f(x_k+1)= f(x_k)+sf'(x_k) + ...,

s ~= -f(x_k)/f'(x_k),

так как f(x_k+1)=> 0 (стремится к нулю).

Метод Ньютона обладает высокой скоростью сходимости. Обычно абсолютная точность решения 10^-5 - 10^-6 достигается через 5-6 итераций.

Недостатком метода является необходимость вычисления на каждой итерации не только левой части уравнения, но и её производной.

Можно, несколько уменьшив скорость сходимости, ограничиться вычислением производной f'(x) только на первой итерации, а затем вычислять лишь значения f(x), не изменяя производной f'(x). Это алгоритм так называемого модифицированного метода Ньютона (рис. 2).

x_k+1 = x_k - f(x_k)/f'(x₀)

Ниже приводится простая консольная программа на Паскале для решения алгебраического уравнения произвольной степени n>1. Функция f(x) и первая производная f'(x) задаются подпрограммами-функциями f и f1 соответственно.

{Метод Ньютона решения нелинейного уравнения}
program Newton;
uses crt; {модуль управления экраном}

function f(x:real):real; {Исходная функция}
begin
 f:=sqr(sqr(x))-5*sqr(x)-x+1;
end;

function f1(x:real):real; {Первая производная функции}
begin
 f1:=4*x*sqr(x)-10*x-1;
end;

var a,b,x,e,en:real;
    i:integer;

begin
 clrscr; {очистить экран}
 writeln ('Решение нелинейного уравнения методом Ньютона');
 writeln ('Уравнение x^4+5x^2-x+1=0');
 write ('Введите левую и правую границы интервала:');
 read (a,b);
 write ('Введите требуемую точность решения:');
 read (e);
 writeln ('Решение:');
 writeln ('Номер шага Значение X');
 en:=abs(a-b);
 x:=b;
 i:=1;
 while (abs(en)>e) do begin {Пока не достигнута точность}
  x:=x-f(x)/f1(x); {выполнить шаг метода}
  writeln (i:10,x:20:14); {вывести значение X с шага}
  en:=abs(x-b); {Новая точность}
  b:=x; {Значение границы для следующего шага}
  i:=i+1; {Номер шага}
 end;
end.

Пример вывода программы:

Решение нелинейного уравнения методом Ньютона
Уравнение x^4+5x^2-x+1=0
Введите левую и правую границы интервала:0 3
Введите требуемую точность решения:0.0001
Решение:
Номер шага Значение X
         1       2.55844155840
         2       2.34660467920
         3       2.29360252760
         4       2.29042173360
         5       2.29041062100

гостевая; E-mail