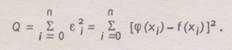Если набор экспериментальных данных получен со значительной погрешностью, то не имеет смысла использовать интерполяцию Лагранжа полиномами и сплайнами для обработки результатов. В этом случае необходимо провести аппроксимирующую кривую, которая не проходит через экспериментальные точки, но в то же время отражает исследуемую зависимость и сглаживает "выбросы", возможные за счет погрешности эксперимента.

Обозначим узлы исходной таблицы данных через х_i, где 0<= i<= n - номер узла. Считаем известными значения экспериментальных данных в узловых точках f(x_i) = f_i. Введем непрерывную функцию φ(х) для аппроксимации дискретной зависимости f(x_i). В узлах функции φ(х) и f(x) будут отличаться на величину е_i = φ(х_i)-f(x_i). Отклонения е_i могут принимать положительные и отрицательные значения. Чтобы не учитывать знаки, возведем каждое отклонение в квадрат и просуммируем квадраты отклонений по всем узлам:

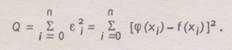(1)

Метод построения аппроксимирующей функции φ(х) из условия минимума величины Q называется методом наименьших квадратов (МНК).

Наиболее распространен способ выбора функции φ(х) в виде линейной комбинации:

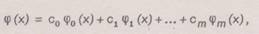(2)

φ₀(х), φ₁(х),…, φ_m(х) - базисные функции; m <= n; c₀, c₁,...,c_m - коэффициенты, определяемые при минимизации величины Q.

Математически условия минимума суммы квадратов отклонений Q запишем, приравнивая нулю частные производные от Q по коэффициентам с_k, 0<=k<=n:

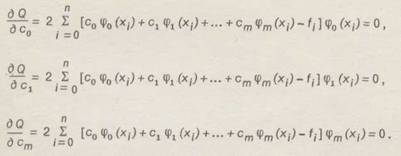(3)

Из системы линейных алгебраических уравнений (3) определяются все коэффициенты с_k. Система (3) называется системой нормальных уравнений. Матрица этой системы имеет следующий вид:

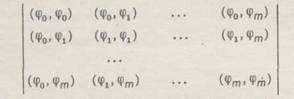(4)

и называется матрицей Грама. Элементы матрицы Грама являются скалярными произведениями базисных функций

(5)

Расширенная матрица системы уравнений (3) получится добавлением справа к матрице Грама столбца свободных членов

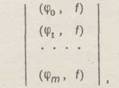(6)

где скалярные произведения, являющиеся элементами столбца, определяются аналогично (5):

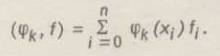(7)

Отметим основные свойства матрицы Грама, полезные при программной реализации алгоритмов МНК:

1) матрица симметрична, т.е. а_i,j = а_j,i, что позволяет сократить объем вычислений при заполнении матрицы;

2) матрица является положительно определенной, следовательно, при решении системы нормальных уравнений методом исключения Гаусса можно отказаться от процедуры выбора главного элемента;

3) определитель матрицы будет отличен от нуля, если в качестве базиса выбраны линейно независимые функции φ_k(х), при этом система (3) имеет единственное решение.

При обработке экспериментальных данных, определенных с погрешностью e в каждой узловой точке, обычно начинают с аппроксимации функцией φ(x), представимой одной-двумя базисными функциями. После определения коэффициентов c_k вычисляют величину Q по формуле (1). Если получится, что корень(Q) > e , то необходимо расширить базис добавлением новых функций φ_k(х). Расширение базиса необходимо осуществлять до тех пор, пока не выполнится условие корень(Q)~=е.

Выбор конкретных базисных функций зависит от свойств аппроксимируемой функции f(x), таких, как периодичность, экспоненциальный или логарифмический характер, свойства симметрии, наличие асимптотики и т.д. На практике чаще всего используется решение, показанное далее.

Степенной базис

Выберем базисные функции φ_k(х) в виде последовательности степеней аргумента х, которые линейно независимы,

(8)

В этом случае мы будем аппроксимировать экспериментальную зависимость полиномом. Степень полинома m выбираем m<<n (при лагранжевой интерполяции m=n). Аппроксимирующая кривая в МНК не проходит через значения исходной функции в узлах, но проведена из условия наименьшего суммарного квадратичного отклонения. Экспериментальные данные "сглаживаются" с помощью функции φ(х). Если же выбрать m=n, то на основании единственности интерполяционного полинома получим функцию φ(х), совпадающую с каноническим интерполяционным полиномом степени n, аппроксимирующая кривая пройдет через все экспериментальные точки и величина Q будет равна нулю. Последнее обстоятельство используется для отладки и тестирования программ, реализующих алгоритмы МНК.

Запишем расширенную матрицу системы нормальных уравнений для базиса (8):

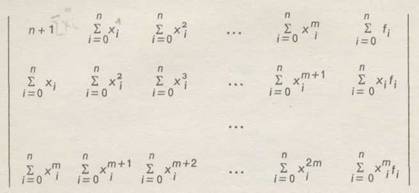(9)

Нетрудно видеть, что для формирования расширенной матрицы (9) достаточно вычислить только элементы первой строки и двух последних столбцов, остальные элементы не являются "оригинальными" и заполняются с помощью циклического присваивания.

Для решения систем уравнений с матрицей Грама разработаны методы сингулярного разложения. Если же m <= 4..5, то такие системы можно решать и более простым методом исключения Гаусса.

Ниже приводится консольная программа на Паскале, реализующая метод МНК со степенным базисом. С клавиатуры вводятся число узлов n, степень полинома m, затем n пар точек (x_i, f_i). После вычисления коээфициентов полинома МНК степени m можно ввести границы по оси X и шаг по X для построения значений полинома.

{Метод наименьших квадратов}
program Mnk;
uses crt; {модуль управления экраном}
type matrix=array[0..100,0..100] of real;
     vector=array [0..100] of real; {Нумеруем точки с нуля}
var n,m,k,i:integer;
    x,f,c:vector;
    a:matrix;
    x0,x9,h,x1:real;
 
procedure InputData (n:integer; var x,f:vector); {Ввод исходных данных}
begin
 for i:=0 to n do begin
  write ('Введите пару значений X(',i,'),F(',i,'):');
  readln (x[i],f[i]);
 end;
end;
 
function ex (a:real; n:integer):real;
 {Показательная функция для формирования матрицы Грама}
var i:integer;
    e:real;
begin
 e:=1;
 for i:=1 to n do e:=e*a;
 ex:=e;
end;
 
procedure Gram (n,m:integer; var x,f:vector; var a:matrix);
{Формирование матрицы Грама A по векторам данных X,F}
var i,j:integer;
    p,q,r,s:real;
begin
 for j:=0 to m do begin
  s:=0; r:=0; q:=0;
  for i:=0 to n do begin
   p:=ex(x[i],j);
   s:=s+p;
   r:=r+p*f[i];
   q:=q+p*ex(x[i],m);
  end;
  a[0,j]:=s;
  a[j,m]:=q;
  a[j,m+1]:=r;
 end;
 {Надо формировать только 1-ю строку и 2 последних столбца матрицы Грама,
  остальные элементы легко получить циклическим копированием:}
 for i:=1 to m do
 for j:=0 to m-1 do a[i,j]:=a[i-1,j+1];
end;
 
procedure Gauss(n:integer; var a:matrix; var x:vector);
{Решение СЛАУ методом Гаусса}
{a - расширенная матрица системы, x - вектор результата}
var i,j,k,l,k1,n1:integer;
    r,s:real;
begin
 {Прямой ход:}
 n1:=n+1;
 for k:=0 to n do begin
  k1:=k+1;
  s:=a[k,k];
  for j:=k1 to n1 do a[k,j]:=a[k,j]/s;
  for i:=k1 to n do begin
   r:=a[i,k];
   for j:=k1 to n1 do a[i,j]:=a[i,j]-a[k,j]*r;
  end;
 end;
 {Обратный ход:}
 for i:=n downto 0 do begin
  s:=a[i,n1];
  for j:=i+1 to n do s:=s-a[i,j]*x[j];
  x[i]:=s;
 end;
end;
 
function fi (m:integer; var c:vector; x1:real):real;
{Аппроксимирующая функция по найденным коэффициентам МНК}
{m - степень полинома, c - вектор коэффициентов,
 x1 - точка, в которой ищем значение}
var i:integer; p:real;
begin
 p:=c[m];
 for i:=m-1 downto 0 do p:=c[i]+x1*p;
 fi:=p;
end;
 
begin
 clrscr; {очистить экран}
 writeln ('Подбор зависимости методом наименьших квадратов');
 write ('Введите число узлов (1<n<100):');
 read (n);
 n:=n-1; {нумерация будет с нуля!}
 write ('Введите степень полинома (1<=m<=',n,'):');
 read (m);
 InputData (n,x,f); {вводим данные}
 Gram (n,m,x,f,a); {считаем матрицу Грама}
 Gauss (m,a,c); {решаем систему линейных уравнений}
 
 writeln ('Коэффициенты полинома МНК ',m,' степени:');
 for i:=0 to m do write (c[i]:10:4);
 writeln;
 
 writeln ('Введите границы по оси X для построения полинома:');
 read (x0,x9);
 writeln ('Введите шаг по X для построения значений полинома:');
 read (h);
 k:=round((x9-x0)/h+1);
 x1:=x0;
 for i:=1 to k do begin
  {строим и выводим полином по найденным коэффициентам}
  writeln (x1:10:4,fi(m,c,x1):10:4);
  x1:=x1+h;
 end;
 reset (input); readln;
end.

Пример вывода программы:

Подбор зависимости методом наименьших квадратов
Введите число узлов (1<n<100):4
Введите степень полинома (1<=m<=3):2
Введите пару значений X(0),F(0):0 0
Введите пару значений X(1),F(1):1 1
Введите пару значений X(2),F(2):2 4
Введите пару значений X(3),F(3):3 9
Коэффициенты полинома МНК 2 степени:
    0.0000    0.0000    1.0000
Введите границы по оси X для построения полинома:
-1 4
Введите шаг по X для построения значений полинома:
1
   -1.0000    1.0000
    0.0000    0.0000
    1.0000    1.0000
    2.0000    4.0000
    3.0000    9.0000
    4.0000   16.0000

гостевая; E-mail